成學

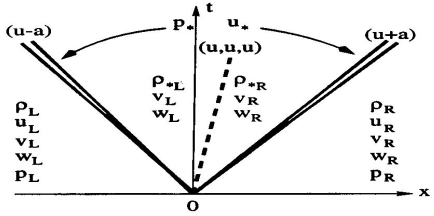
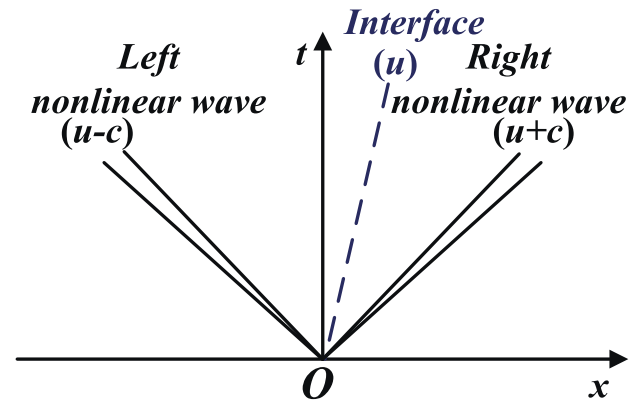
Conservative MethodsGodunov's First-Order Upwind Method$$ u^{n+1}_i = u^n_i + \frac{\Delta t}{\Delta x}\left[ f_{i-1/2} - f_{i+1/2} \right] $$Godunov's first-order upwind method는 위의 식의 intercell numerical flux $f_{i+1/2}$를 구할 때, local Riemann problem의 solution을 활용함. 이는 현재시간 $n$에서 값들이 piece-wise constant distribution이라는 것을 바탕으로 함.Intecell boundary $x_{i+1/2}$에서 discontinuity에 의해 분리되어 있는 constant ..

IntroductionHigh-resolution upwind와 centred numerical methods를 hyperbolic conservation laws에 적용하기 위해 필요한 background를 다룸.  아Discretisation: Introductory ConceptsNumerical method는 PDE로 표현되는 continuous problem을 finite set of discrete values로 대체함. PDE의 domain을 mesh 또는 grid로 나누어 finite set of points 이나 volumes로 분할하는 과정이 필요하며, 이를 통해 discrete values를 얻을 수 있음.이산화방법 중에서 FDM과 FVM을 사용할 수 있는 데, FDM은 grid po..

Multi-Dimensional Euler Equations3차원의 convervation-law를 differential form으로 표현하면 다음과 같음.$$ \mathbf{U}_t + \mathbf{F(U)}_x + \mathbf{G(U)}_y + \mathbf{H(U)}_z = 0 $$ $$ \mathbf{U} = [\rho, \rho u, \rho v, \rho w, E]^\text{T} $$ $$ \mathbf{F} = [\rho u, \rho u^2 + p, \rho u v, \rho u w, u(E+p)]^\text{T} $$ $$ \mathbf{G} = [\rho v, \rho u v, \rho v^2 + p, \rho v w, v(E+p)]^\text{T} $$ $$ \mathbf{H}..

One-Dimensional Euler EquationsEuler equation은 압축성 medium에 대한 body force, viscosity, heat conduction 영향을 무시함으로써 얻을 수 있음.Conservative와 non-conservative 수식을 활용하여 이상기체 EOS에 대한 1차원 time-dependent Euler equations를 얻을 수 있음. Conservative FormulationEuler equation의 conservative formulation을 differential form으로 표현하면 다음과 같음. $$ \mathbf{U}_t + \mathbf{F(U)}_x = 0, $$$$ \mathbf{U} = [\rho, \rho u, E]^\text{..

Conservation Laws$m$개의 conservation laws의 시스템은 아래와 같이 conserved variables vector $\mathbf{U}$와 flux vector $\mathbf{F(U)}$를 활용하여 표현할 수 있음. $$ \mathbf{U}_t + \mathbf{F(U)}_x = 0 $$만약, jacobian matrix $\mathbf{A(U)}=\partial \mathbf{F} / \partial \mathbf{U}$가 real eigenvalues $\lambda_i(\mathbf{U})$와 linearly independent eigenvectors $\mathbf{K}^{(i)}(\mathbf{U})$를 가지면, 해당 시스템을 hyperbolic이라고 함.※ E..

Introduction본 장에서는 아래의 이유로 hyperbolic PDEs와 hyperbolic conservation laws를 구체적으로 다룸.Viscosity와 heat conduction을 무시한 Euler equation이 hyperbolic system임.PDE의 hyperbolic항에 이산화 기법를 적용할 때 가장 엄격한 요구사항이 필요함.  Quasi-Linear Equations: Basic ConceptsDependent variables $u_t$와 independent variables $x,t$가 포함된 first-order partial differential equations (PDE) system은 아래와 같음. \[ \frac{\partial u_i}{\partial t}..

When I finish reading the book, the related posts will be made public.Preface Pattern recognition has its origins in engineering, whereas machine learning grew out of computer science. However, these activities can be viewed as two facets of the same field, and together they have undergone substantial development over the past ten years.

IntroductionEquation of state로 주어지는 closure condition과 함께, compressible material의 dynamics에 대한 governing equation을 위해 ① 미분방정식으로 표현되는 Euler equation, ② 열역학적 고려사항, ③ viscous diffusion, ④ heat transfer, ⑤ 적분방정식으로 표현되는 Euler equation에 대해서 각각 다룸.NotationDot product of two vectors $\mathbf{A} = \left(a_1, a_2, a_3\right)$ and $\mathbf{B} = \left(b_1, b_2, b_3\right)$ → scalar$$\mathbf{A \cdot B} = a_1..

The related posts are expected to be made public by the end of January.I will only cover Chapters 1, 2, 3, and 5 of this book. PrefaceL. F. Richardson's work had the four distinguishing characteristics of CFD, which remain the pillars of modern CFD.PRACTICAL PROBLEM to solve MATHEMATICAL MODEL to represent the problem in the partial differential equation formNUMERICAL METHODCOMPUTERCFD is the sc..