Conservation Laws
- $m$개의 conservation laws의 시스템은 아래와 같이 conserved variables vector $\mathbf{U}$와 flux vector $\mathbf{F(U)}$를 활용하여 표현할 수 있음.
$$ \mathbf{U}_t + \mathbf{F(U)}_x = 0 $$- 만약, jacobian matrix $\mathbf{A(U)}=\partial \mathbf{F} / \partial \mathbf{U}$가 real eigenvalues $\lambda_i(\mathbf{U})$와 linearly independent eigenvectors $\mathbf{K}^{(i)}(\mathbf{U})$를 가지면, 해당 시스템을 hyperbolic이라고 함.
※ Eigenvalue와 eigenvector가 $\mathbf{U}$에 의존하지만, 편의를 위해 $\mathbf{U}$를 생략
Integral Forms of Conservation Laws
- Conservation laws를 integral form으로 나타내는 두 가지 장점이 있음.
- 지배방정식의 유도가 control volume에서의 integral relation으로 표현되는 물리적 보존 원리에 기반함.
- Integral formulation은 solution이 less smoothness해도 되기 때문에, discontinuous solution을 포함할 수 있음.
Integral Form I
- 1차원에서의 mass conservation에 대한 integral equation은 아래와 같으며, $f=\rho u$로 표현되는 flux가 포함됨.
$$ \frac{d}{dt}\int_{x_\text{L}}^{x_\text{R}}\rho(x,t)dx = f(x_\text{L},t)- f(x_\text{R},t) $$
- Complete system에 대해서, flux vector $\mathbf{F(U)}$를 활용하여, 다음과 같이 표현할 수 있음.
\[
\frac{d}{dt}\int_{x_\text{L}}^{x_\text{R}} \mathbf{U}(x, t) \, dx
= \mathbf{F}(\mathbf{U}(x_\text{L}, t)) - \mathbf{F}(\mathbf{U}(x_\text{R}, t))
\]
Integral Form II
- 위의 식을 $t_1$와 $t_2$사이의 시간에 대해 적분하면 다음과 같이 표현할 수 있음.
\[
\int_{t_1}^{t_2} \left[ \frac{d}{dt} \int_{x_\text{L}}^{x_\text{R}} \mathbf{U}(x, t) \, dx \right] dt
= \int_{x_\text{L}}^{x_\text{R}} \mathbf{U}(x, t_2) \, dx
- \int_{x_\text{L}}^{x_\text{R}} \mathbf{U}(x, t_1) \, dx
\]
\[
\int_{x_\text{L}}^{x_\text{R}} \mathbf{U}(x, t_2) \, dx
= \int_{x_\text{L}}^{x_\text{R}} \mathbf{U}(x, t_1) \, dx
+ \int_{t_1}^{t_2} \mathbf{F}(\mathbf{U}(x_\text{L}, t)) \, dt
- \int_{t_1}^{t_2} \mathbf{F}(\mathbf{U}(x_\text{R}, t)) \, dt
\]
Integral Form III
- $x-t$ space의 *any domain에서의 미분방정식을 적분하고 Green's theorem을 통해 얻을 수 있음.
*Integral form II는 Integral form III에서,
control volume $V$를 rectangle shape으로 한 special case
Non-Linearities and Shock Formation
- Non-linear hyperbolic conservation law는 *wave steepening과 shock formation과 같은 특징을 가지고 있으며, scalar에 대한 식은 characteristic speed $\lambda$를 포함하여 아래와 같음.
$$ u_t + f(u)_x = 0, \quad u(x, 0) = x_0(x) $$
$$ u_t + \lambda(u)u_x = 0, \quad \lambda(u) = \frac{df}{du}=f'(u) $$
*이와 관련된 물리적 현상은 compressible media에서 발생하는 shock wave가 있음.
- Flux function $f(u)$는 conservation law solution $u(x,t)$에 큰 영향을 미치며, characteristic speed $\lambda(u)$의 monotonicity가 중요한 특징임.
- $u$에 대해 monotone increasing function $\lambda'(u)=f''(u) > 0$ → convex flux vector
- $u$에 대해 monotone decreasing function $\lambda'(u)=f''(u) < 0$ → concave flux vector
- some $u$에 대해서 extrema $ \lambda'(u)=f''(u) = 0 $ → non-convex and non-concave flux vector
Construction of Solutions on Characteristics
- Characteristics $x=x(t)$가 IVP $dx/dt = \lambda(u), \ x(0)=x_0$를 만족할 때, $u$와 $x$가 $t$의 함수라고 하면, curve $x(t)$를 따라 $u$의 total derivative는 다음과 같음.
$$ \frac{du}{dt} = u_t + \lambda(u)u_x = 0 $$- 즉, $u$는 IVP를 만족하는 characterisitics를 따라 일정하므로, characteristic의 slope $\lambda(u)$도 일정함. 따라서 characteristics는 straight line이 됨.
Wave Steepening

- Linear advection의 경우, characteristic speed가 $a$로 일정하기 때문에, distortion 없이 $a$의 속도로 초기 initial data $u_0(x)$가 전파됨.
- Non-linear advection의 경우, characteristics $\lambda(u)$가 solution의 함수이기 때문에, distortion이 발생함.
- Flux function $f(u)$가 convex이면, characteristic speed는 $u$에 대해서 increasing function임. 따라서, initial data $u_0(x)$가 큰 값을 가지면, 더욱 빠르게 전파됨.
- $x_0^{(1)} < x_0^{(2)} < x_0^{(3)} $이라고 하면, 전파 속도가 점점 빨라지기 때문에, 시간이 지남에 따라 기존의 interval이 broader 하고 flatter profile로 변하게 됨. 이를 expansive region이라고 하며, 해당 영역에서는 $x$가 증가할수록, characteristic speed가 증가함.
- 반대로 $ x_0^{(3)} > x_0^{(4)} > x_0^{(5)} $의 값을 가지면, 전파 속도가 점점 느려지기 때문에 *compressive region이라고 함. 해당 영역에서는 시간이 지남에 따라, 기존 profile이 steeper 하고 narrower 해짐.
- Flux vector가 concave인 경우, 위의 상황은 반대로 나타남.
- Flux function $f(u)$가 convex이면, characteristic speed는 $u$에 대해서 increasing function임. 따라서, initial data $u_0(x)$가 큰 값을 가지면, 더욱 빠르게 전파됨.
*Compressive region에서 characteristics가 교차하게 되면,
이를 wave breaks라고 하며, 미분값 $u_x$은 무한대의 값을 가지게 됨.
- Pure advection 외에도 viscous dissipation과 heat conduction을 포함하기 위해, flux function은 $u_x$에 의존해야하며, 이에 따라 modified conservation law는 다음과 같이 표현할 수 있음.
$$ u_t +f(u)_x =\alpha u_{xx} $$- $u$의 시간에 대한 변화율이 advection term $f(u)_x$ 뿐만 아니라, diffusion term $\alpha u_{xx}$에 대해서도 영향을 받음.
Shock Waves
- 물리적으로, shock wave는 압력, 밀도, 온도와 같은 물리량이 급격히 변화하는 small transition layer임. 강한 shock의 transition layer는 대략 $10^{-7}$m의 분자 mean-free path와 유사한 규모를 가짐. 따라서, *이러한 shock을 mathematical discontinuity로 대체하는 것은 타당함.
*Sonic boom과 같이 매우 약한 shock wave의 경우,
discontinuous approximiation이 부정확함.
- $x-t$ plane에서 solution $u(x, t)$이 jump discontinuity 하는 line을 $ x_\text{L} < s = s(t) < x_\text{R} $라고 하고, control volume에 대한 integral form의 conservation law는 아래와 같이 표현할 수 있음.
\[
f(u(x_\text{L}, t)) - f(u(x_\text{R}, t))
= \frac{d}{dt} \int_{x_\text{L}}^{s(t)} u(x, t) \, dx
+ \frac{d}{dt}\int_{s(t)}^{x_\text{R}} u(x, t) \, dx
\] \[
\begin{aligned}
f(u(x_\text{L}, t)) - f(u(x_\text{R}, t)) &= \left[ u(s_\text{L}, t) - u(s_\text{R}, t) \right] S \\
&\quad + \int_{x_\text{L}}^{s(t)} u_t(x, t) \, dx
+ \int_{s(t)}^{x_\text{R}} u_t(x, t) \, dx
\end{aligned}
\]- $u(s_\text{L}, t)$는 $x$가 왼쪽에서 $s(t)$를 향할 때 $u(s(t), t)$의 극한
- $u(s_\text{R}, t)$는 $x$가 오른쪽에서 $s(t)$를 향할 때 $u(s(t), t)$의 극한
- $S=ds/dt$는 discontinuity의 speed
- $u_t(x, t)$가 bounded 되어 있기 때문에 좌우에서 $s(t)$로 접근할 때, 적분은 사라져 Rankine-Hugoniot condition으로 정리할 수 있음.
\[
f(u(x_\text{L}, t)) - f(u(x_\text{R}, t))
= \left[ u(s_\text{L}, t) - u(s_\text{R}, t) \right] S
\]
$$ \Delta f = S \Delta u $$
Two Examples of Discontinuous Solutions
- Riemann problem에서, $u_\text{L}> u_\text{R} $이고 flux vector가 convex일 때, characteristic speed는 right region보다 left region에서 더 빠름 (compressive data).
- 즉, $\lambda_\text{L} \equiv \lambda(u_\text{L}) > \lambda_\text{R} \equiv \lambda(u_\text{R})$이며, initial data는 compressive되어, 즉각적으로 characteristics가 교차하는 현상이 발생함.
- Rankine-Hugoniot condition에 의해 speed of the discontinuity를 구할 수 있으며, 이 discontinuous solution을 shock wave라고 함. 이는 다음의 entropy condition을 만족함.
\[
\lambda(u_\text{L}) > S > \lambda(u_\text{R})
\]
- 반대로, $u_\text{L} < u_\text{R}$일 때는 data가 expansive data가 됨.
- Discontinuity로부터 characteristics가 diverge 하는 rarefaction shock, entropy-violating shock이 발생하기 때문에 물리적으로 올바르지 않으며, 위의 entropy condition을 만족하지 못함.
- 데이터의 expansive 특성을 고려할 때, 초기 데이터가 시간이 지남에 따라 broaden해지는 것이 타당함.
Rarefaction Waves

- Entropy-violating solution이 physical solution으로서 거부되는 주된 이유는 *instability 때문임.
*Instability는 초기 데이터의 작은 perturbation이 solution의 큰 변화를 야기하는 것을 의미
- 이를 위해, $u_\text{L}$에서 $u_\text{R}$로의 discontinuous change를 $u_0(x)$의 linear variation으로 바꿈으로써 initial data를 다음과 같이 수정할 수 있음.\[
u_0(x) =
\begin{cases}
u_\text{L}, & x \leq x_\text{L}, \\
u_\text{L} + \frac{u_\text{R} - u_\text{L}}{x_\text{R} - x_\text{L}} (x - x_\text{L}), & x_\text{L} < x \leq x_\text{R}, \\
u_\text{R}, & x \geq x_\text{R}.
\end{cases}
\]- Solution은 두 개의 constant states $u_\text{L}, u_\text{R}$와, 두 값 사이의 smooth transition 영역을 포함함. 이를 rarefaction wave라고 함.
- Rarefaction wave의 오른쪽 edge는 $x_\text{R}$에서 나오는 characteristic에 의해 주어지며, 이를 Head of the rarefaction이라고 함. 이는 $u_0(x_\text{R})=u_R$의 값을 전달함.
- 왼쪽 edge는 $x_\text{L}$에서 나오는 characteristic에 의해 주어지며, 이는 Tail of the rarefaction이라고 함.
- Solution은 두 개의 constant states $u_\text{L}, u_\text{R}$와, 두 값 사이의 smooth transition 영역을 포함함. 이를 rarefaction wave라고 함.
- Convexity를 가정할 때, 높은 값의 $u_0(x)$은 더욱 빠르게 전파하기 때문에 wave는 시간이 지남에 따라, spread 되고 flatten 됨. Wave의 spreading은, constant coefficient를 가지는 linear hyperbolic system에서는 볼 수 없는, 전형적인 non-linear 현상임.
- Dicontinuous data가 퍼지는 interval의 size $\Delta x = x_\text{R} - x_\text{L}$가 아무리 작아도, rarefaction solution의 구조는 변하지 않음. 또한, instability를 야기하는 rarefaction shock solution과는 완전히 다름.
- Rarefaction wave solution은 stable 하며, $x_\text{L}$과 $x_\text{R}$이 각각 0으로 접근하면, IVP에서 제시된 $x=0$에서의 discontinuous data로 돌아감.
- 이는 $u_0(x)$가 $x=0$에서 $x_\text{L}$과 $x_\text{R}$사이의 모든 값을 가지고, 그렇기에 $\lambda(u_0(x))$가 $x=0$에서 $\lambda_\text{L}$과 $\lambda_\text{R}$사이의 모든 값을 가진다는 것을 의미함. 따라서, initial data는 즉시 분해되고 rarefaction solution을 일으키게 됨.
- 모든 characteristics가 sinlge point로부터 나오는 것을 centred rarefaction wave라고 함.
- Rarefaction wave solution은 stable 하며, $x_\text{L}$과 $x_\text{R}$이 각각 0으로 접근하면, IVP에서 제시된 $x=0$에서의 discontinuous data로 돌아감.
- 물리적으로 정확한 solution과 잘못된 solution을 구별하기 위해 물리적인 discontinuity가 Rankine-Hugoniot 외에도 entopry condition을 만족해야 함.
Characteristic Fields
- Real eigenvalues $\lambda_i(\mathbf{U})$와 이에 따른 right eigenvectors $\mathbf{K}^{(i)}(\mathbf{U})$를 가지는 hyperbolic system에서, characteristic speed $\lambda_i(\mathbf{U})$는 charcteristic field $\lambda_i$-field를 정의하며, 이는 또한 $\mathbf{K}^{(i)}$-field라고도 함.
Def. Linearly degenerate fields
- 아래의 식을 만족하면, $\lambda_i$-characterisitic field는 linearly degenerate 하다고 함.
$$ \nabla \lambda_i(\mathbf{U}) \cdot \mathbf{K}^{(i)}(\mathbf{U}) = 0, \quad \forall \mathbf{U}\in \mathcal{R}^{m} $$- Linear system에서는 eigenvalues가 constant이기 때문에 $\nabla \lambda_i(\mathbf{U})=0$임. 따라서, constnat coefficients를 가지는 linear hyperbolic system의 모든 characteristic field는 linearly degenerate 함.
Def. Genuinely nonlinear fields
- 아래의 식을 만족하면, $\lambda_i$-characterisitic field는 genuinely nonlinear 하다고 함. $$ \nabla \lambda_i(\mathbf{U}) \cdot \mathbf{K}^{(i)}(\mathbf{U}) \neq 0, \quad \forall \mathbf{U}\in \mathcal{R}^{m} $$
Rankine-Hugoniot Conditions

- Hyperbolic conservation law의 $\lambda_i$-characteristic field와 관련된 discontinuous wave speed를 $S_i$라고 할 때, Rankine-Hugoniot condition은 아래와 같음.
$$ \Delta \mathbf{F} = S_i \Delta \mathbf{U} $$- 일정한 coefficient를 가지는 linear system에 대해서, wave speed $S_i=\lambda_i$에 대한 Rankine-Hugoniot condtion은 아래와 같으며, 이를 통해 일정한 coefficient를 가지는 linear hyperbolic system에 대한 Riemann problem solution을 더욱 직접적으로 구할 수 있음.
$$ \Delta \mathbf{F} = \mathbf{A} \Delta \mathbf{U} = \lambda_i(\Delta \mathbf{U})_i $$
- 일정한 coefficient를 가지는 linear system에 대해서, wave speed $S_i=\lambda_i$에 대한 Rankine-Hugoniot condtion은 아래와 같으며, 이를 통해 일정한 coefficient를 가지는 linear hyperbolic system에 대한 Riemann problem solution을 더욱 직접적으로 구할 수 있음.
Generalised Riemann Invariants
$$ \mathbf{W}_t + \mathbf{A(W)W}_x = 0 $$
$$ \mathbf{W} = \left[ w_1, w_2, \dots, w_m \right]^\text{T} $$
$$ \mathbf{K}^{(i)} = \left[ k_1^{(i)}, k_2^{(i)} , \dots, k_m^{(i)} \right]^\text{T} $$
- General quasi-linear hyperbolic system과 이 system의 right eigenvector가 위와 같을 때, Generalised Riemann Invariants는 다음과 같은 $m-1$개의 ordinary differential equations의 관계로 주어짐.
$$ \frac{dw_1}{k_1^{(i)}} = \frac{dw_2}{k_2^{(i)}} = \dots = \frac{dw_m}{k_m^{(i)}} $$
Example: Linearised Gas Dynamics
- Gas dynamics의 linearised equation에 대한 generalised riemann invariants는 다음과 같은 과정으로 구할 수 있음.
$$ \mathbf{W}=[w_1, w_2]^\text{T} = [\rho, u]^\text{T} $$ $$ \mathbf{K}^{(1)} = [\rho_0, -a]^\text{T}, \quad \mathbf{K}^{(2)} = [\rho_0, a]^\text{T} $$- $\lambda_1$-wave를 걸쳐서 다음이 성립함.
$$ \frac{d\rho}{\rho_0} = \frac{du}{-a} $$ $$ du+\frac{a}{\rho_0}d \rho = 0 $$ $$ \therefore I_\text{L}(\rho, u) = u + \frac{a}{\rho_0}\rho=\text{constant across }\lambda_1\text{-wave} $$ - $\lambda_2$-wave를 걸쳐서 다음이 성립함.
$$ \frac{d\rho}{\rho_0} = \frac{du}{a} $$ \[ \therefore I_\text{R}(\rho, u) = u - \frac{a}{\rho_0} \rho = \text{constant across } \lambda_2 \text{-wave} \]
- $\lambda_1$-wave를 걸쳐서 다음이 성립함.
Elementary-Wave Solutions of Riemann Problem
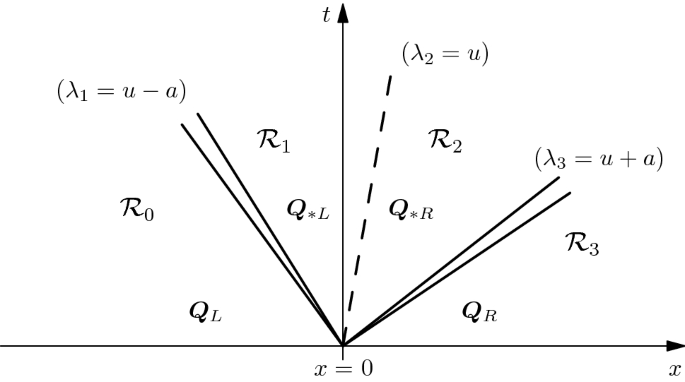
- 일정한 coefficient를 가지는 linear system에서, 각 wave는 discontinuity of speed $S_i = \lambda_i$이며, linearly degenerate field를 정의함.
- Non-linear system에서, wave들은 shock wave와 contact wave와 같은 discontinuity 또는 rarefaction과 같은 smooth trainsition wave가 될 수 있음.
- Riemann problem solution에 포함된 wave의 type은 closure condition에 의해 크게 의존함. Euler equation의 경우, equation of state만을 고려하기 때문에, 오직 shock, contact, rarefaction의 wave만 존재함.

Shock wave
- Shock wave에서는, 두 개의 일정한 상태 $\mathbf{U}_\text{L}$과 $\mathbf{U}_\text{R}$가 genuinely non-linear field $i$의 single jump discontinuity에서 연결되어 있으며, 다음의 조건들을 만족함.
- Rankine-Hugoniot conditions: $\mathbf{F(U_\text{R} )}- \mathbf{F(U_\text{L} )} = S_i\left(\mathbf{U}_\text{R} - \mathbf{U}_\text{L} \right)$
- Entropy condition: $ \lambda_i(\mathbf{U}_\text{L}) > S_i > \lambda_i(\mathbf{U}_\text{R}) $
- 위 그림의 (a)에 묘사되어 있는 것처럼, wave의 양 쪽에 있는 characterisitic $dx/dt = \lambda_i$가 shock wave로 합쳐지며, 이는 shock의 compressive 특징을 보여줌.
Contact wave
- Contact wave에서는, 두 개의 일정한 상태 $\mathbf{U}_\text{L}$과 $\mathbf{U}_\text{R}$가 linearly degenerate field $i$의 single jump discontinuity에서 연결되어 있으며, 다음의 조건들이 성립됨.
- Rankine-Hugoniot conditions: $ \mathbf{F}(\mathbf{U}_\text{R}) - \mathbf{F}(\mathbf{U}_\text{L}) = S_i \left( \mathbf{U}_\text{R} - \mathbf{U}_\text{L} \right) $
- Wave에 걸쳐서, Generalised Riemann Invariants의 constancy: $ \frac{dw_1}{k_1^{(i)}} = \frac{dw_2}{k_2^{(i)}} = \dots = \frac{dw_m}{k_m^{(i)}} $
- Parallel characteristic condition: $ \lambda_i(\mathbf{U}_\text{L}) = \lambda_i(\mathbf{U}_\text{R}) = S_i$
- 위 그림의 (b)에 묘사되어 있는 것처럼, wave의 양 쪽에 있는 characterisitics는 contact discontinuity와 평행함.
Rarefaction wave
- Rarefaction wave에서는, 두 개의 일정한 상태 $\mathbf{U}_\text{L}$과 $\mathbf{U}_\text{R}$가 genuinely non-linear field $i$의 smooth transition에서 연결되어 있으며, 다음의 조건들을 만족함.
- Wave에 걸쳐서, Generalised Riemann Invariants의 constancy: $ \frac{dw_1}{k_1^{(i)}} = \frac{dw_2}{k_2^{(i)}} = \dots = \frac{dw_m}{k_m^{(i)}} $
- Divergence of characteristics: $ \lambda_i(\mathbf{U}_\text{L}) < \lambda_i(\mathbf{U}_\text{R}) $
- 위 그림의 (c)에 묘사되어 있는 것처럼, wave의 양 쪽에 있는 characterisitics는 wave 안의 characteristics처럼 diverge 함.
※ General Riemann problem의 solution은 shock wave, contact discontinuities, rarefaction wave 중 어느 것도 될 수 있는 m개의 wave를 포함함. General Riemann problem을 풀 때는, wave의 구체적인 type을 구별하여 필요한 condition들을 enforce 해야 함.
'Book > Riemann Solvers & Numerical Methods' 카테고리의 다른 글
| [Book Note] Ch 3. Some Properties of the Euler Equations (2) (0) | 2025.01.14 |
|---|---|
| [Book Note] Ch 3. Some Properties of the Euler Equations (1) (0) | 2024.12.27 |
| [Book Note] Ch 2. Notions on Hyperbolic Partial Differential Equations (1) (0) | 2024.12.11 |
| [Book Note] Ch 1. Equations of Fluid Dynamics (0) | 2024.12.05 |
| [Book Note] Riemann Solvers and Numerical Methods for Fluid Dynamics (0) | 2024.12.03 |