Multi-Dimensional Euler Equations
- 3차원의 convervation-law를 differential form으로 표현하면 다음과 같음.
$$ \mathbf{U}_t + \mathbf{F(U)}_x + \mathbf{G(U)}_y + \mathbf{H(U)}_z = 0 $$ $$ \mathbf{U} = [\rho, \rho u, \rho v, \rho w, E]^\text{T} $$ $$ \mathbf{F} = [\rho u, \rho u^2 + p, \rho u v, \rho u w, u(E+p)]^\text{T} $$ $$ \mathbf{G} = [\rho v, \rho u v, \rho v^2 + p, \rho v w, v(E+p)]^\text{T} $$ $$ \mathbf{H} = [\rho w, \rho u w, \rho v w, \rho w^2 + p, w(E+p)]^\text{T} $$ - Conservation laws의 integral form은 다음과 같음.
$$ \frac{d}{dt}\iiint_V \mathbf{U}dV + \iint_A \mathcal{H}\cdot \mathbf{n}dA = 0$$- 위의 식은 volume $V$ 안 $\mathbf{U}$의 시간 변화율은 control volume의 boundary $A$를 통해서 들어오는 total flux에만 의존한다는 것을 의미함. Finite volume method는 이 방정식에 기반함.
Two-Dimensional Equations in Coservative Form
- 2차원의 Euler equation을 differential conservative form으로 표현하면 다음과 같음.
$$ \mathbf{U}_t + \mathbf{F(U)}_x + \mathbf{G(U)}_y = 0 $$ $$ \mathbf{U} = [\rho, \rho u, \rho v, E]^\text{T} $$ $$ \mathbf{F} = [\rho u, \rho u^2 + p, \rho u v, u(E+p)]^\text{T} $$ $$ \mathbf{G} = [\rho v, \rho u v \rho v^2 + p, v(E+p)]^\text{T} $$- Flux $\mathbf{F(U)}$에 해당하는 Jacobian matrix의 eigenvalues와 right eigenvectors는 다음과 같음. $$ \lambda_1 = u-a, \quad \lambda_2 = \lambda_3 = u, \quad \lambda_4 = u+a $$ $$ \mathbf{K}^{(1)} = [1, u-a, v, H-au]^\text{T} \quad \mathbf{K}^{(2)} = [1, u, v, 0.5\mathbf{V}^2]^\text{T} $$ $$ \mathbf{K}^{(3)} = [0, 0, 1, v]^\text{T} \quad \mathbf{K}^{(4)} = [1, u+a, v, H+ua]^\text{T} $$
Rotational Invariance
- Euler equation의 rotational invariance 특성을 바탕으로, Cartesian direction에 놓이지 않는 domain을 처리할 수 있음.
- 2차원에서의 surface $A$에 수직인 outward unit vector $\mathbf{n}$은 다음과 같이, normal vector $\mathbf{n}$와 x축과의 각도인 $\theta$를 활용하여 다음과 같이 표현할 수 있음. $$ \mathbf{n} \equiv (n_1, n_2) \equiv (\cos\theta, \sin\theta) $$
- 따라서, 아래의 surface integral의 integrand는 다음과 같이 표현할 수 있음. $$ \frac{d}{dt}\iiint_V \mathbf{U}dV + \iint_A (\mathbf{F}, \mathbf{G})\cdot \mathbf{n}dA = 0$$ $$ (\mathbf{F}, \mathbf{G})\cdot\mathbf{n} = \cos\theta\mathbf{F(U)} + \sin\theta\mathbf{G(U)} $$
Proposition: Rotational Invariance
- 2차원 Euler equation은 모든 angles $\theta$에 대해서 다음의 rotational invariance property를 만족함. 여기서 $\mathbf{T} = \mathbf{T}(\theta)$는 rotation matrix 임. $$ \cos\theta\mathbf{F(U)} + \sin\theta\mathbf{G(U)} = \mathbf{T}^\text{-1}\mathbf{F(TU)} $$ \[
\mathbf{T} =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & \cos\theta & \sin\theta & 0 \\
0 & -\sin\theta & \cos\theta & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
\]
Def. Hyperbolicity in Time
- 모든 admissible state $\mathbf{U}$과 real angle $\theta$에 대해서 matrix $\mathbf{A}(\mathbf{U}, \theta) = \cos\theta\mathbf{A(U)} + \sin\theta\mathbf{B(U)}$가 diagonalisable 하면, 해당 system은 time에서 hyperbolic 함.
- 따라서, two-dimensional Euler equations는 시간 domain에서 hyperbolic 함. (증명 생략)
Proposition: Types of Characteristic Fields
- $i=1, 4$의 characteristic fields는 genuinely non-linear이고, $i=2, 3$은 linearly degenerate임.
- Riemann problem의 맥락에서, 2와 3 waves를 거쳐 pressure와 normal velocity component $u$는 constant임. Field 2는 contact discontinuity와 관련이 있고, 이를 거쳐서 density가 불연속적으로 jump함. Field 3은 shear wave와 관련 있으며, 이를 거쳐서 tangential velocity component가 불연속적으로 jump함. 1과 4 characteristic fields는 shock wave와 rarefaction wave와 관련 있음.
Three-Dimensional Equations in Conservative Form
Eigenstructure
$$ \mathbf{U}_t + \mathbf{F(U)}_x + \mathbf{G(U)}_y + \mathbf{H(U)}_z = 0 $$
- Flux $\mathbf{F(U)}$에 해당하는 Jacobian matrix의 eigenvalues와 right eigenvectors는 다음과 같음. $$ \lambda_1 = u-a, \quad \lambda_2 = \lambda_3 = \lambda_4 = u, \quad \lambda_5 = u+a $$ \[
\mathbf{K} =
\begin{bmatrix}
1 & 1 & 0 & 0 & 1 \\
u-a & u & 0 & 0 & u+a \\
v & v & 1 & 0 & v \\
w & w & 0 & 1 & w \\
H-ua & 0.5\mathbf{V}^2 & v & w & H+ua
\end{bmatrix}
\]
Proposition: Rotational Invariance
- Time-dependent three dimensional Euler equation은 rotationally invariant이므로 모든 angles $\theta^{(y)}, \theta^{(z)}$에 대해서 다음의 식을 만족함. $$ \cos\theta^{(y)}\cos\theta^{(z)}\mathbf{F(U)} + \cos\theta^{(y)}\sin\theta^{(z)}\mathbf{G(U)}+\sin\theta^{(y)}\mathbf{H(U)} = \mathbf{T^{-1}F(TU)} $$
- $\mathbf{T} = \mathbf{T}(\theta^{(y)}, \theta^{(z)})$는 rotation matrix이며, 두개의 rotation matrices의 product 임. $$ \mathbf{T} = \mathbf{T}(\theta^{(y)}, \theta^{(z)}) = \mathbf{T}^{(y)}\mathbf{T}^{(z)} $$
Three-Dimensional Primitive Variable Formulation
Proposition: Primitive Variable
- 3차원 time-dependent Euler equation도 primitive variables $\mathbf{W} = [\rho, u, v, w, p]^\text{T}$로 표현할 수 있음. $$ \rho_t + u \rho_x + v\rho_y + w\rho_z +\rho(u_x + v_y + w_z) = 0, $$ $$ u_t + uu_x + vu_y + wu_z + 1/\rho p_x = 0 $$ $$ v_t + uv_x + vv_y + wv_z + 1/\rho p_y = 0 $$ $$ w_t + uw_x + vw_y + ww_z + 1/\rho p_z = 0 $$ $$ p_t + up_x + vp_y + wp_z + \rho a^2 (u_x + v_y + w_z) = 0. $$
Proposition: Eigenvalues and Eigenvectors
$$ \lambda_1 = u-a, \quad \lambda_2 = \lambda_3 = \lambda_4 = u, \quad \lambda_5 = u+a $$
$$ \mathbf{K}^{(1)} = [\rho, -a, 0, 0, \rho a^2]^\text{T} \quad \mathbf{K}^{(2)} = [1, 0, v, w, 0]^\text{T} \quad \mathbf{K}^{(3)} = [\rho, 0, 1, w, 0]^\text{T} $$
$$ \mathbf{K}^{(4)} = [\rho, 0, v, 1, 0]^\text{T} \quad \mathbf{K}^{(5)} = [\rho, a, 0, 0, \rho a^2]^\text{T} $$
The Split Three-Dimensional Riemann Problem
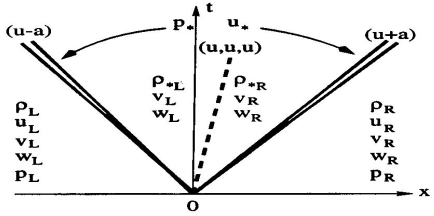
- 대부분의 upwind method를 통해, 2차원 또는 3차원 Euler equation을 풀 때, split Riemann problem의 solution이 필요함. *$x$-split 3차원 Riemann problem은 다음과 같음. $$ \mathbf{U}_t + \mathbf{F(U)}_x = 0, $$ \[ \mathbf{U}(x,0) = \mathbf{U}^{(0)}(x) = \begin{cases} \mathbf{U}_\text{L}, & \text{if } x < 0, \\ \mathbf{U}_\text{R}, & \text{if } x > 0.
\end{cases} \] $$ \mathbf{U} = [\rho, \rho u, \rho v, \rho w, E]^\text{T} $$ $$ \mathbf{F(U)} = [\rho u, \rho u^2 + p, \rho u v, \rho u w, u(E+p)]^\text{T} $$- Star region에서의 middle wave를 거쳐서 pressure와 normal particle velocity는 constant 함. 여기서, middle wave에는 $\lambda_3 = \lambda_4 = u$와 관련된 새로운 characteristic fields가 존재하는 데, 이 shear wave를 가로질러 tangential velocity component $v$와 $w$가 불규칙하게 변함. (이러한 tangential velocity components는 일부 approximate Riemann solvers에 의해 부정확하게 modeling 됨.)
- 1차원 case와 동일하게, 1과 5의 characteristic fields는 genuinely non-linear이며, 이는 rarefactions과 shock wave와 관련됨. 1과 5 rarefaction or shock waves에 대한 Generalised Riemann Invariants를 통해 tangential velocity components $v$와 $w$의 변화가 없음을 확인할 수 있음.
*Split 3차원 방정식에 대한 Riemann problem solution을 찾는 것은
1차원 Riemann problem의 solution을 찾는 것과 본질적으로 동일함.
Conservative vs. Non-Conservative Formulations
- Smooth solution 가정 하에서, conservative와 non-conservative formulations은 다르지 않음 (not unique).
- Conservative formulations은 주의 깊게 분석해야 할 필요가 있는데, 순전히 수학적 관점에서만 conservative 일 수 있기 때문임. 따라서, 보존되는 quantities가 무엇인지 확인하고, 물리적으로 타당한지 판단해야 함.
※ Shock wave가 있을 때, 순전히 수학적으로만 conervative 한 formulations은
wrong shock speed를 야기하고, 따라서 wrong solutions을 만들어 냄.
One-dimensional shallow water
- Mass와 momentum에 대한 물리적 conservation laws는 다음과 같이 표현할 수 있음. \[
\begin{bmatrix}
\phi \\
\phi u
\end{bmatrix}_t
+
\begin{bmatrix}
\phi u \\
\phi u^2 + \frac{1}{2}\phi^2
\end{bmatrix}_x
= 0
\] - Smooth solution 가정하에서, 다음과 같은 식 전개를 통해 new conservation-law form을 유도할 수 있음. $$ \phi_t + u\phi_x + \phi u_x = 0 $$ $$ u_t + uu_x + \phi_x = 0 $$ \[
\begin{bmatrix}
\phi \\
u
\end{bmatrix}_t
+
\begin{bmatrix}
\phi u \\
\frac{1}{2}u^2 + \phi
\end{bmatrix}_x
= 0
\]- 위의 system은 수학적으로 보존되며, mass conservation과 particle speed conservation을 표현하지만, 물리적으로는 보존되지 않음 (shock wave가 존재할 때 잘못된 solution을 야기).
Proposition: Shock Wave Solution
- Conventional conservative form에 대한 right-facing shock wave solution은 다음과 같음. $$ S = u_\text{R} + Q/\phi_\text{R} $$ \[
Q = \left[\frac{1}{2}(\phi_* + \phi_\text{R})\phi_*\phi_\text{R}\right]^{\frac{1}{2}}
\] - New conservative form에 대한 right-facing shock wave solution은 다음과 같음. $$ \hat{S} = u_\text{R} + \hat{Q}/\phi_\text{R} $$ \[
\hat{Q} = \left[ \frac{2}{\phi_* + \phi_\text{R}} \right]^{\frac{1}{2}}\phi_*\phi_\text{R}
\]- Shock wave가 trivial 할 때만 $(\phi_* \equiv \phi_\text{R})$, $S$ 와 $\hat{S}$가 동일함. 일반적으로 $\hat{S}\le S$이기 때문에, new conservation laws의 shock solution은 conventional conservation laws의 shock solution보다 느림. 또한, new conservation laws는 non-unique 함.
'Book > Riemann Solvers & Numerical Methods' 카테고리의 다른 글
| [Book Note] Ch 5. Notions of Numerical Methods (2) (4) | 2025.01.14 |
|---|---|
| [Book Note] Ch 5. Notions of Numerical Methods (1) (0) | 2025.01.14 |
| [Book Note] Ch 3. Some Properties of the Euler Equations (1) (0) | 2024.12.27 |
| [Book Note] Ch 2. Notions on Hyperbolic Partial Differential Equations (2) (0) | 2024.12.13 |
| [Book Note] Ch 2. Notions on Hyperbolic Partial Differential Equations (1) (0) | 2024.12.11 |