成學

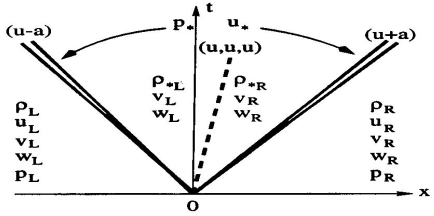
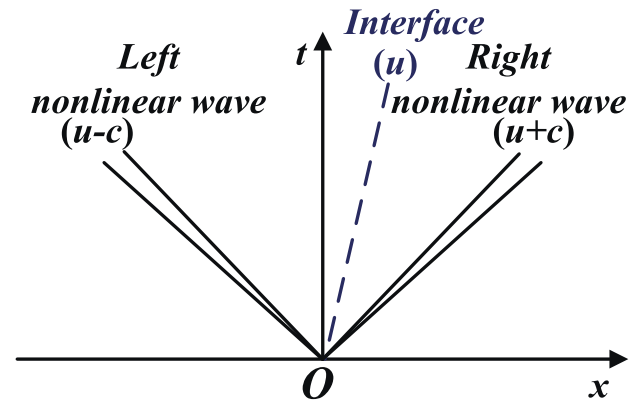
Multi-Dimensional Euler Equations3차원의 convervation-law를 differential form으로 표현하면 다음과 같음.$$ \mathbf{U}_t + \mathbf{F(U)}_x + \mathbf{G(U)}_y + \mathbf{H(U)}_z = 0 $$ $$ \mathbf{U} = [\rho, \rho u, \rho v, \rho w, E]^\text{T} $$ $$ \mathbf{F} = [\rho u, \rho u^2 + p, \rho u v, \rho u w, u(E+p)]^\text{T} $$ $$ \mathbf{G} = [\rho v, \rho u v, \rho v^2 + p, \rho v w, v(E+p)]^\text{T} $$ $$ \mathbf{H}..

One-Dimensional Euler EquationsEuler equation은 압축성 medium에 대한 body force, viscosity, heat conduction 영향을 무시함으로써 얻을 수 있음.Conservative와 non-conservative 수식을 활용하여 이상기체 EOS에 대한 1차원 time-dependent Euler equations를 얻을 수 있음. Conservative FormulationEuler equation의 conservative formulation을 differential form으로 표현하면 다음과 같음. $$ \mathbf{U}_t + \mathbf{F(U)}_x = 0, $$$$ \mathbf{U} = [\rho, \rho u, E]^\text{..

IntroductionEquation of state로 주어지는 closure condition과 함께, compressible material의 dynamics에 대한 governing equation을 위해 ① 미분방정식으로 표현되는 Euler equation, ② 열역학적 고려사항, ③ viscous diffusion, ④ heat transfer, ⑤ 적분방정식으로 표현되는 Euler equation에 대해서 각각 다룸.NotationDot product of two vectors $\mathbf{A} = \left(a_1, a_2, a_3\right)$ and $\mathbf{B} = \left(b_1, b_2, b_3\right)$ → scalar$$\mathbf{A \cdot B} = a_1..