Introduction
- 본 장에서는 아래의 이유로 hyperbolic PDEs와 hyperbolic conservation laws를 구체적으로 다룸.
- Viscosity와 heat conduction을 무시한 Euler equation이 hyperbolic system임.
- PDE의 hyperbolic항에 이산화 기법를 적용할 때 가장 엄격한 요구사항이 필요함.
Quasi-Linear Equations: Basic Concepts
- Dependent variables $u_t$와 independent variables $x,t$가 포함된 first-order partial differential equations (PDE) system은 아래와 같음. \[ \frac{\partial u_i}{\partial t} + \sum_{j=1}^m a_{ij}(x,t,u_1,\dots,u_m) \frac{\partial u_j}{\partial x} + b_i(x,t,u_1,\dots,u_m) = 0 \]
- Matrix form으로 표현하면 다음과 같음.
$$ \mathbf{U}_t + \mathbf{AU}_x + \mathbf{B} = 0 $$ $$ \mathbf{U} = [u_1, u_2, ..., u_m]^\text{T}, \mathbf{B} = [b_1, b_2, ..., b_m]^\text{T} $$ \begin{equation}
\mathbf{A} =
\begin{bmatrix}
a_{11} & \dots & a_{1m} \\
a_{21} & \dots & a_{2m} \\
\vdots & \ddots & \vdots \\
a_{m1} & \dots & a_{mm}
\end{bmatrix}
\end{equation}- Constant $a_{ij}, b_i$ → linear with constant coefficient
- $a_{ij}=a_{ij}(x,t), b_i =b_{i}(x,t)$ → linear with variable coefficient
- $\mathbf{A} = \mathbf{A(U)}$ → quasi-linear
- Equation의 solution을 얻기 위해 independent variable $x,t$의 범위를 지정해야 함.
- $x_l < x < x_r$로 정의되는 영역은 PDE의 spatial domain이라고 하며, $(x_l, x_r)$을 위해서 boundary condition이 필요함.
- 시간에 대해서도 $t_0 < t < \infty$를 정의하며, initial time $t_0$을 지정하기 위해 initial condition이 필요함.
- PDE의 예시
- Linear advection (constant $a$는 wave propagation speed)
$$ \frac{\partial u}{\partial t} + a \frac{\partial u}{\partial x} = 0 $$ - Inviscid Burgers equation $(a=a(u)=u)$
$$ \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} = 0 $$
- Linear advection (constant $a$는 wave propagation speed)
Def. Conservation Laws
- Conservation laws는 다음과 같이 정의되는 PDE system임.
$$ \mathbf{U}_t + \mathbf{F(U)}_x = 0 $$ $$ \mathbf{U} = [u_1, u_2, ..., u_m] $$ $$ \mathbf{F(U)} = [f_1, f_2, ..., f_m] $$- $\mathbf{U}$: conserved variable vector
- $\mathbf{F=F(U)}$: flux vector.
- $f_i$: $\mathbf{U}$의 요소 $u_j$의 함수
Def. Jacobian Matrix
- Flux vector의 jacobian matrix는 다음과 같음.
\begin{equation}
\mathbf{A} =
\begin{bmatrix}
\frac{\partial f_1}{\partial u_1} & \dots & \frac{\partial f_1}{\partial u_m} \\
\frac{\partial f_2}{\partial u_1} & \dots & \frac{\partial f_2}{\partial u_m} \\
\vdots & \ddots & \vdots \\
\frac{\partial f_m}{\partial u_1} & \dots & \frac{\partial f_m}{\partial u_m}
\end{bmatrix}
\end{equation}
- Chain rule을 적용하여 conservative laws를 quasi-linear form으로 표현할 수 있음.
$$ \frac{\partial \mathbf{F(U)}}{\partial x} = \frac{\partial \mathbf{F}}{\partial \mathbf{U}} \frac{\partial \mathbf{U}}{\partial x} $$
$$ \mathbf{U}_t + \mathbf{A(U)U}_x = 0 $$
$$ \text{Linear advection:} \quad \frac{\partial u}{\partial t} + \frac{\partial f(u)}{\partial x} = 0, \quad f(u) = au$$
$$ \text{Inviscid Burgers:} \quad \frac{\partial u}{\partial t} + \frac{\partial f(u)}{\partial x} = 0, \quad f(u)=1/2u^2$$
Def. Eigenvalues
- Eigenvalue는 위의 characteristic polynomial의 해로 정의함.
$$ |\mathbf{A}-\lambda \mathbf{I}| = \text{def}(\mathbf{A} - \lambda \mathbf{I}) = 0 $$- 물리적으로, eigenvalue는 정보의 전파 속도를 나타내며, $x$가 증가하는 방향으로 positive가 되고, 감소하는 방향으로 negative가 됨.
- Linear advection equation의 eigenvalue는 $\lambda =a$이고, inviscid Burgers equation의 eigenvalue는 $\lambda = u$임.
Def. Eigenvectors
- Eigenvalues $\lambda_i$에 해당하는 right eigenvector는 $\mathbf{K}^{(i)}=\left[k_1^{(i)}, k_2^{(i)} , ..., k_m^{(i)} \right]^\text{T}$이며, $ \mathbf{A} \mathbf{K}^{(i)} = \lambda_i \mathbf{K}^{(i)} $를 만족함.
- 유사하게, eigenvalues $\lambda_i$에 해당하는 left eigenvector는 $ \mathbf{L}^{(i)} = \begin{bmatrix} l_1^{(i)}, l_2^{(i)}, \dots, l_m^{(i)} \end{bmatrix}^\text{T} $이며, $ \mathbf{L}^{(i)} \mathbf{A} = \lambda_i \mathbf{L}^{(i)} $를 만족함.
Def. Hyperbolic System
- 시스템의 jacobian matrix가 real eigenvalues $\lambda_1, ..., \lambda_m$을 가지고, 이에 해당하는 right eigenvectors $\mathbf{K}^{(1)},...,\mathbf{K}^{(m)} $가 linearly independent → hyperbolic
- 모든 eigenvalue $\lambda_i$가 모두 distinct → strictly hyperbolic
- No real eigenvalue → elliptic
Linear Advection Equation (LAE)
- 3차원 공간에서의 time-dependent linear advection equation은 다음과 같음.
$$ u_t + a(x,y,z,t)u_x + b(x,y,z,t)u_y + c(x,y,z,t)u_z = 0 $$- Coefficients $a, b, c$가 충분히 smooth하다고 가정하면, source term을 가진 conservation law로 표현할 수 있음.
$$ u_t + (au)_x + (bu)_y + (cu)_z = u(a_x + b_y + c_z) $$ - Linear advection equation을 initial-value problem (IVP)으로 표현하면 다음과 같음.
- Coefficients $a, b, c$가 충분히 smooth하다고 가정하면, source term을 가진 conservation law로 표현할 수 있음.
\[ \begin{aligned} \text{PDE:} & \quad u_t + a u_x = 0, \quad -\infty < x < \infty, \quad t > 0, \\ \text{IC:} & \quad u(x, 0) = u_0(x). \end{aligned} \]
- Linear first-order ordinary differential equation (ODE)를 통해서 hyperbolic conservation laws에 대한 numerical methods를 분석할 수 있음.
$$ \frac{dx}{dt}=\beta, \quad x=x(t), \quad \beta=\text{constant} $$
Characteristics and General Solution
- Characteristics는 $t-x$ plane에서의 곡선 $x=x(t)$로 정의되며, 이 선을 따라 PDE는 ODE가 됨.

- $x=x(t)$이고, $u$가 $t$에 대한 함수라고 할 때, $u=u(x(t),t)$, characteristics $x=x(t)$를 따라 $u$의 시간 변화율을 구할 수 있음.
$$ \frac{du}{dt} = \frac{\partial u}{\partial t} + \frac{dx}{dt} \frac{\partial u}{\partial x} $$ - Characteristics가 ODE $dx/dt=a$를 만족하면, 다음과 같이 정리할 수 있음.
$$ \frac{du}{dt} = \frac{\partial u}{\partial t} + a \frac{\partial u}{\partial x} =0 $$ - 따라서, characteristics를 따라 $u$의 변화율은 0이며, 이는 $u$가 해당 선을 따라서 일정하다는 것을 의미함. *이때 $a$는 characteristic speed라고 하며, $t-x$ plane에서의 선 $x=x(t)$의 기울기를 의미함.
- $x=x(t)$이고, $u$가 $t$에 대한 함수라고 할 때, $u=u(x(t),t)$, characteristics $x=x(t)$를 따라 $u$의 시간 변화율을 구할 수 있음.
- 여러개의 characteristics가 $x-t$평면 상에서 정의되는데, 초기 시간에서의 initial condition $(\text{e.g., } x(0)=x_0)$이 결정되면, 하나의 characteristics로 정해질 수 있음. 이 characteristics는 초기지점 $(x_0, 0)$을 통과하기 때문에 다음의 식으로 표현가능함.
$$ x=x_0+at $$ - Characteristics를 따라서 $u$가 일정하게 유지되기 때문에, $u$가 초기조건 $u(x,0)=u_0(x)$으로 주어진다면, characteristics $x(t)=x_0+at$를 따라서 solution은 다음과 같음.
$$ u(x,t) = u_0(x_0) = u_0(x-at) $$- 이를 해석하면, initial profile $u_0(x)$가 주어지면, PDE는 velocity $a$의 속도로 profile을 그대로 유지하며 $a>0$이면, 오른쪽으로, $a<0$이면, 왼쪽으로 전파함. 즉, initial profile이 변하지 않고 유지됨.
- 이러한 wave propagation에서 wave는 유한한 속도로 움직이는 disturbance로 이해할 수 있음.
*실용적으로는 $x-t$ plane을 흔히 사용하기 때문에, characteristics의 slope는 $1/a$이 됨.
※ Constant coefficient를 가지는 linear hyperbolic PDE의 characteristics는 평행함.
Riemann Problem

- 아래의 식은 Riemann problem이라고 불리는 특별한 IVP로, 초기 상태는 $x=0$에서 불연속함.
\[ \begin{aligned} \text{PDE:} & \quad u_t + a u_x = 0, \\[5pt] \text{IC:} & \quad u(x, 0) = u_0(x) = \begin{cases} u_\text{L}, & x < 0, \\ u_\text{R}, & x > 0. \end{cases} \end{aligned} \]- Linear advection equation에서의 solution을 통해 알수있듯, initial profile의 어떤 지점에서도 $d=at$로 전파됨. 따라서, Riemann problem에서도 $x=0$에서의 초기 불연속 point가 $d=at$로 전파됨.
- *불연속을 전파하는 characteristics $x=at$는 $u_\text{L}$을 solution으로 하는 왼쪽 영역과 $u_\text{R}$를 solution으로 하는 오른쪽 영역으로 나눔. 이를 수식으로 표현하면 다음과 같음.
\[ u(x, t) = u_0(x-at) = \begin{cases} u_\text{L}, & x-at < 0, \\ u_\text{R}, & x-at > 0. \end{cases} \]
*Riemann problem에서 $x=0$을 통과하는 characteristic은 중요한데,
이를 기준으로 solution이 변하기 때문임.
Linear Hyperbolic Systems
- Single linear advection equation을 확장하여, $m$개의 equation으로 이루어진 hyperbolic PDEs는 다음과 같이 표현할 수 있음.
$$ \mathbf{U}_t + \mathbf{AU}_x = 0 $$- Hyperbolicity 가정에 따라서, $\mathbf{A}$는 $m$개의 real eigenvalues $\lambda_i$와 $m$개의 linearly independent eigenvectors $\mathbf{K}^{(i)}$를 가짐.
Diagonalisation and Characteristic Variables
Def. Diagonalisable System
- Matrix $\mathbf{A}$가 아래의 식과 같이, diagonal matrix $\mathbf{\Lambda}$와 matrix $\mathbf{K}$로 표현되면, diagonalisable하다고 함.
\[
\mathbf{A} = \mathbf{K} \mathbf{\Lambda} \mathbf{K}^{-1} \quad \text{or} \quad \mathbf{\Lambda} = \mathbf{K}^{-1} \mathbf{A} \mathbf{K}
\] \begin{equation}
\mathbf{\Lambda} =
\begin{bmatrix}
\lambda_1 & \dots & 0 \\
0 & \dots & 0 \\
\vdots & \vdots & \vdots \\
0 & \dots & \lambda_m
\end{bmatrix}
\end{equation} $$ \mathbf{K}=[\mathbf{K}^{(1)}, ..., \mathbf{K}^{(m)} ] $$ $$ \mathbf{AK}^{(i)} =\lambda_i \mathbf{K}^{(i)}$$- Diagonal matrix $\mathbf{ \Lambda }$는 eigenvalues $\lambda_i$로 이루어져 있음.
- Matrix $\mathbf{K}$는 right eigenvector $\mathbf{K}^{(i)}$로 이루어져 있음.
Characteristic variables
- Right eigenvector의 inverse matrix를 활용하면 characteristic variables $\mathbf{W} = [w_1, w_2, ..., w_m]^\text{T}$로 system을 표현할 수 있음. 이를 통해 linear system $ \mathbf{U}_t + \mathbf{AU}_x = 0 $는 completely decoupled됨.
\[
\mathbf{W} = \mathbf{K}^{-1} \mathbf{U} \quad \text{or} \quad \mathbf{U} = \mathbf{K} \mathbf{W}
\]- Characteristic variables로 표현하기 위해 $\mathbf{U}_t = \mathbf{KW}_t, \mathbf{U}_x = \mathbf{KW}_x$를 적용함. $$ \mathbf{KW}_t + \mathbf{AKW}_x = 0 $$ $$ \mathbf{W}_t + \mathbf{\Lambda W}_x = 0 $$
- 위의 식을 system의 canonical form 또는 characteristic form이라고 함. 이 system의 $i$번째 PDE는 다음과 같으며, single unknown $w_i(x,t)$만을 포함하고 있기 때문에 decoupled system임.
$$ \frac{\partial w_i}{\partial t} + \lambda_i \frac{\partial w_i}{\partial x} = 0 $$ - Characteristic speed는 $\lambda_i$이며, $m$개의 ODE를 만족하는 $m$개의 characteristic가 존재함.
General Initial-Value Problem
- Linear hyperbolic system에 대한 initial condition이 $ \mathbf{U}^{(0)} = \left( u_1^{(0)}, ..., u_m^{(0)} \right)^\text{T} $로 주어질 때, canonical system을 풀어 IVP의 general solution을 구할 수 있음. Characteristic variable로 정의되는 initial condition과 canonical form의 solution은 아래와 같음.
\[
\mathbf{W}^{(0)} = \mathbf{K}^{-1} \mathbf{U}^{(0)} \quad \text{or} \quad \mathbf{U}^{(0)} = \mathbf{K} \mathbf{W}^{(0)}
\]
$$ w_i(x,t) = w_i^{(0)}(x-\lambda_i t) $$
- $\mathbf{U=KW}$의 역변환을 통해 original variable에 대한 solution을 구할 수 있음.
\[ \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_m \end{bmatrix} = \begin{bmatrix} k_1^{(1)} & k_1^{(2)} & \dots & k_1^{(m)} \\ k_2^{(1)} & k_2^{(2)} & \dots & k_2^{(m)} \\ \vdots & \vdots & \ddots & \vdots \\ k_m^{(1)} & k_m^{(2)} & \dots & k_m^{(m)} \end{bmatrix} \begin{bmatrix} w_1 \\ w_2 \\ \vdots \\ w_m \end{bmatrix} \] $$ \mathbf{U}(x,t) = \sum_{i=1}^m w_i(x,t)\mathbf{K}^{(i)} $$ $$ \mathbf{U}(x,t) = \sum_{i=1}^m w_i^{(0)}(x-\lambda_i t) \mathbf{K}^{(i)} $$- 이는 함수 $w_i(x,t)$가 vector $\mathbf{U}$의 eigenvector expansion에서 $\mathbf{K}^{(i)}$의 coefficient를 의미함.
- $x-t$ plane 내의 점 $(x,t)$에서의 solution $\mathbf{U}(x, t)$는 $m$개의 points $x_0^{(i)}=x-\lambda_i t$에서의 initial data에만 의존하며, 각각은 $x$축과의 교차점을 의미함.
- Solution $\mathbf{U}$는 $m$개의 waves의 superposition으로 생각할 수 있고, 각 wave는 형태의 변화없이 독립적으로 전파됨. 즉, $i$번째 wave는 $w_i^{(0)}(x)\mathbf{K}^{(i)}$ shape을 가지며, $\lambda_i$의 속도로 전파함.
Riemann Problem
- Hyperbolic, constant coefficient system에 대한 Riemann problem은 다음과 같음.
\[
\begin{aligned}
\text{PDEs:} & \quad \mathbf{U}_t + \mathbf{A} \mathbf{U}_x = 0, \quad -\infty < x < \infty, \quad t > 0, \\[5pt]
\text{IC:} & \quad \mathbf{U}(x, 0) = \mathbf{U}^{(0)}(x) =
\begin{cases}
\mathbf{U}_\text{L}, & x < 0, \\
\mathbf{U}_\text{R}, & x > 0.
\end{cases}
\end{aligned}
\]- Strictly hyperbolic이라고 가정하면, real and distinct eigenvalue는 다음의 order를 가짐.
$$ \lambda_1 < \lambda_2 < \dots < \lambda_m $$
General Solution

- 시스템에 대한 Riemann problem의 solution은 위의 그림과 같이 주어짐. 이는 원점에서 나오는 $m$개의 wave로 구성되어 있으며, 각각은 eigenvalue $\lambda_i$의 속도로 전파하는 jump discontinuity를 의미함.
- $\lambda_1$ wave의 왼쪽 solution은 $\mathbf{U}_\text{L}$
- $\lambda_m$ wave의 오른쪽 solution은 $\mathbf{U}_\text{R}$
- Eigenvectors $\mathbf{K}^{(1)}, \dots, \mathbf{K}^{(m)}$은 linearly independent하기 때문에, left solution $\mathbf{U}_\text{L}$과 right solution $\mathbf{U}_\text{R}$은 다음과 같이 right eigenvectors의 선형조합으로 표현할 수 있음.
$$ \mathbf{U}_\text{L} = \sum^m_{i=1}\alpha_i \mathbf{K}^{(i)}, \quad \mathbf{U}_\text{R} = \sum^m_{i=1}\beta_i \mathbf{K}^{(i)} $$
- Eigenvectors $\mathbf{K}^{(1)}, \dots, \mathbf{K}^{(m)}$은 linearly independent하기 때문에, left solution $\mathbf{U}_\text{L}$과 right solution $\mathbf{U}_\text{R}$은 다음과 같이 right eigenvectors의 선형조합으로 표현할 수 있음.
- 얻어야 할 solution은 $\lambda_1$과 $\lambda_m$사이의 solution
- Characteristic variable에 대해, $m$개의 scalar Riemann problems을 가짐.
$$ \frac{\partial w_i}{\partial t} + \lambda_i\frac{\partial w_i}{\partial x} = 0 $$ \[
w_i^{(0)}(x) =
\begin{cases}
\alpha_i, & x < 0, \\
\beta_i, & x > 0.
\end{cases}
\] - 따라서, scalar Riemann problem의 solution은 아래와 같이 표현할 수 있음.
\[
w_i(x, t) = w_i^{(0)}(x-\lambda_i t) =
\begin{cases}
\alpha_i, & x-\lambda_i t < 0, \\
\beta_i, & x-\lambda_i t > 0.
\end{cases}
\] - 주어진 point $(x,t)$에 대해서, $\lambda_I < x/t < \lambda_{I+1}$를 만족하는 eigenvalue $\lambda_I$가 있다고 하면, 즉 $x-\lambda_it>0, i<I$이라면, original variables에 대한 Riemann problem의 solution은 다음과 같음.
$$ \mathbf{U}(x,t) = \sum^m_{i=I+1}\alpha_i\mathbf{K}^{(i)}+\sum^I_{i=1}\beta_i\mathbf{K}^{(i)} $$
- Characteristic variable에 대해, $m$개의 scalar Riemann problems을 가짐.
Solution for 2$\times$2 System
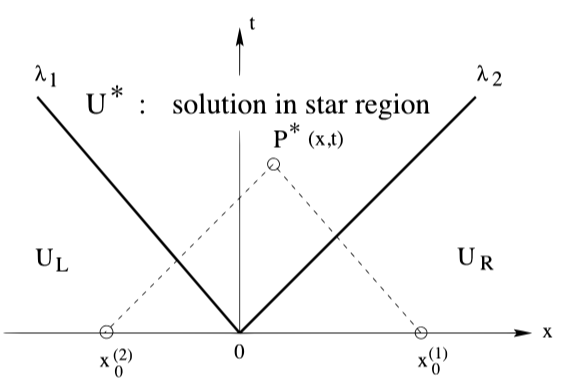
- 2$\times$2 linear system에 solution은 다음과 같이 표현할 수 있음.
- Left side의 solution: $ \mathbf{U}_\text{L} = \alpha_1 \mathbf{K}^{(1)} + \alpha_2 \mathbf{K}^{(2)} $
- *Right side의 solution: $ \mathbf{U}_\text{R} = \beta_1 \mathbf{K}^{(1)} + \beta_2 \mathbf{K}^{(2)} $
- 중간의 solution은 star region에 존재하며, $\mathbf{U^*}$로 표기함.
- Initial point $x_0^{(2)}=x-\lambda_2 t$와 $x_0^{(1)}=x-\lambda_1 t$를 통과하는 characteristics는 star region의 한 point $\mathbf{P^*}(x,t)$를 지나감.
- Left solution region으로부터 right solution region으로 horizontal line $(t=t^*)$을 따라 이동하면서 solution의 변화를 확인해보면, 가장 먼저, $dx/dt = \lambda_1$의 wave를 지나게 됨. 이는 initial value $x-\lambda_1 t$가 negative에서 positive로 바뀌기 때문에 $\alpha_1$이 $\beta_1$로 변함. 따라서, star region에서의 solution은 다음과 같음.
$$ \mathbf{U^*}(x,t)=\beta_1 \mathbf{K}^{(1)} + \alpha_2 \mathbf{K}^{(2)}$$
- 한편, solution $\mathbf{U}$의 jump (변화량)은 다음과 같이 표현할 수 있음.
$$ \Delta \mathbf{U} = \mathbf{U}_\text{R}-\mathbf{U}_\text{L} = (\beta_1 - \alpha_1)\mathbf{K}^{(1)} + \dots + (\beta_m - \alpha_m)\mathbf{K}^{(m)} $$- Wave $i$를 건너면서 변화하는 $\mathbf{U}$의 jump는 wave $i$의 wave strength $\beta_i - \alpha_1$를 활용하여 표현할 수 있음. $$ (\Delta \mathbf{U})_i = (\beta_i - \alpha_i)\mathbf{K}^{(i)} $$
*$dx/dt=\lambda_2$의 wave를 지나게 되면,
initial value $x-\lambda_2 t$도 negative에서 positive로 바뀌기 때문에
모든 coefficient $\alpha$가 $\beta$로 됨.
Def. Domain of Dependence
- *Point $P=(x^*,t^*)$의 domain of dependence를 point $x_0$라고 하며, 2$\times$2 system에서 domain of dependence는 point $P$를 지나는 characteristics가 통과할 수 있는 $x$축의 interval인 $[x_\text{L}, x_\text{R}]$임. 즉, slowest와 fastest characteristics에 의해 결정되고, bounded됨.
*Point $P=(x^*,t^*)$에서의 solution은 오로지 initial data $x_0$에만 의존함.
즉, solution은 initial data $u_0(x)$의 값과 동일
Def. Domain of Determinacy
- Domain of dependence가 $[x_\text{L}, x_\text{R}]$로 주어질 때, domain of determinacy는 solution $\mathbf{U}(x,t)$이 존재할 수 있는 domain안에서의 set of points $(x,t)$를 의미함.
Def. Rnage of Influence
- $x$축 위의 한 점 $Q=(x_0, 0)$의 range of influence는 해당 점의 intial data에 의해 영향을 받는 solution $\mathbf{U}(x, t)$이 존재하는 set of points $(x, t)$를 의미함.
'Book > Riemann Solvers & Numerical Methods' 카테고리의 다른 글
| [Book Note] Ch 3. Some Properties of the Euler Equations (2) (0) | 2025.01.14 |
|---|---|
| [Book Note] Ch 3. Some Properties of the Euler Equations (1) (0) | 2024.12.27 |
| [Book Note] Ch 2. Notions on Hyperbolic Partial Differential Equations (2) (0) | 2024.12.13 |
| [Book Note] Ch 1. Equations of Fluid Dynamics (0) | 2024.12.05 |
| [Book Note] Riemann Solvers and Numerical Methods for Fluid Dynamics (0) | 2024.12.03 |