Introduction
- High-resolution upwind와 centred numerical methods를 hyperbolic conservation laws에 적용하기 위해 필요한 background를 다룸.
아Discretisation: Introductory Concepts
- Numerical method는 PDE로 표현되는 continuous problem을 finite set of discrete values로 대체함. PDE의 domain을 mesh 또는 grid로 나누어 finite set of points 이나 volumes로 분할하는 과정이 필요하며, 이를 통해 discrete values를 얻을 수 있음.
- 이산화방법 중에서 FDM과 FVM을 사용할 수 있는 데, FDM은 grid point에서 정의되는 point values를 활용하고 FVM은 finite volume의 average value를 활용함.
Approximation to Derivatives

- Taylor's theorem을 통해서 아래의 식을 얻을 수 있음. $$ g(x_0 + \Delta x) = g(x_0) + \sum_k \frac{(\Delta x)^k}{k!}g^{(k)}(x_0) $$
- Taylor series를 truncation하여 $g(x_0 + \Delta x)$의 근사값을 얻을 수 있고, $g(x)$의 미분값에 대한 근사값도 얻을 수 있음. $$ g(x_0 + \Delta x) = g(x_0) + \Delta xg^{(1)}(x_0) + \frac{(\Delta x)^2}{2}g^{(2)}(x_0) + O(\Delta x^3) $$ $$ g^{(1)}(x_0) = \frac{g(x_0 + \Delta x) - g(x_0)}{\Delta x} + O(\Delta x) $$
- 이를 one-sided approximation (upwind methods)이라고 하며, forward finite difference approximation이라고도 함. 이와 유사하게 backward first-order approximation은 다음과 같음. \[
g(x_0 - \Delta x) = g(x_0) - \Delta x g^{(1)}(x_0) + \frac{(\Delta x)^2}{2} g^{(2)}(x_0) + O(\Delta x^3)
\] $$ g^{(1)}(x_0) = \frac{g(x_0) - g(x_0 - \Delta x)}{\Delta x} + O(\Delta x) $$ - 위의 forward와 backward를 합치면 아래와 같이, central finite-difference approximation을 얻을 수 있으며 이는 second-order accurate을 가짐. \[
g^{(1)}(x_0) = \frac{g(x_0 + \Delta x) - g(x_0 - \Delta x)}{2\Delta x} + O(\Delta x^2)
\]
Finite Difference Approximation to a PDE
- FDM을 활용하여 PDE ($u_t + au_x = 0$)를 근사화하면 아래와 같이 표현할 수 있음. 즉, differential equation이 finite difference equation으로 대체됨. 아래의 식은 시간에 대해서 first-order forward approximation를, 공간에 대해서 second-order central approximation를 적용함. $$ \frac{u^{n+1}_i - u^{n}_i}{\Delta t} + a \left[ \frac{u^n_{i+1} - u^n_{i-1}}{2 \Delta x} \right] = 0 $$
- 현재 time level $n$의 값들은 known이기 때문에, 새로운 time level인 $n+1$에서의 값을 표현하는 single unknown $u^{n+1}_i$에 대한 식으로 전개할 수 있음 (explicit scheme). $$ u^{n+1}_i = u^n_i -\frac{1}{2}c\left[u^n_{i+1} - u^n_{i-1} \right] $$ $$ c = \frac{\Delta t a}{\Delta x} = \frac{a}{\Delta x / \Delta t} $$
- $c$는 Courant number로 알려진 무차원량이며, CFL number (Courant-Friedrichs-Lewy number)라고도 함. 이는 partial differential equation (PDE)에서의 wave propagation speed $a$와 domain discretization에서 정의된 grid speed $\Delta x / \Delta t$의 ratio로 생각할 수 있음.
※ 위의 식은 von Neumann stability analysis를 통해서 unconditionally unstable함.
Selected Difference Schemes
First Order Upwind Scheme
- Stable한 결과를 얻기 위해 공간에 대해서 central approximation이 아닌 first-order one-sided approximation을 적용함. one-sided approximation를 적절히 활용하기 위해서는 wave propagation speed $a$의 부호를 고려해야 함.
- $a$가 양수의 값을 가지는 경우에는 아래의 식으로 표현할 수 있는데, 이를 first-order *upwind method (≡ CIR scheme)라고 함. $$ u_x = \frac{u^n_i - u^n_{i-1}}{\Delta x} $$ $$ u_i^{n+1} = u^n_i - c \left( u_i^n - u^n_{i-1} \right) $$
* Upwind (or upstream): 공간 차분을 수행할 때,
information(wind)이 불어오는 방향의 mesh point를 사용함.
(e.g., positive $a$일 때 upwind는 left이고, negative $a$일 때 upwind는 right)
※ 위의 식은 von Neumann stability를 통해 $0 \le c \le 1$의 CFL 조건하에서 stable함.
즉, 해당 scheme은 conditionally stable함.
- CFL은 wave speed $a$와 mesh spacing $\Delta x$와 time step size $\Delta t$에 따라 변하기 때문에, $a$가 주어져 있다면, 원하는 정확도와 computing 자원에 따라 적절한 $\Delta x$를 선택할 수 있음. $\Delta t$도 CFL condition를 만족하도록 제한해야 함.
- CIR scheme은 wave speed의 부호에 따라 다른 방향으로의 discretisation이 수행됨.
- Positivie $a$에 대해서 downwind method를 적용하면 아래와 같음. $$ u_i^{n+1} = u^n_i - c \left( u_{i+1}^n - u^n_{i} \right) $$
- 해당 식은 positive $a$에 대해서 unconditionally unstable 하지만, negative $a$에 대해서는 upwind scheme이기 때문에 conditionally stable함. 따라서, 공간차분을 수행할 때 wave speed $a$의 부호를 고려해야 함.
- First-order upwind scheme을 아래의 general form으로 표현할 수 있음. $$ u^{n+1}_i = u^n_i - c^{+}\left( u^n_i - u^n_{i-1} \right) - c^{-} \left( u^n_{i+1} - u^n_{i} \right) $$ $$ 0 \le \left\vert c\right\vert \le 1 $$
[CIR scheme's stencil figure!!, i will update it]
- PDE의 solution $u(x_i, t^{n+1})$은 characteristics speed $dx/dt=a$를 따라서 일정하기 때문에 $u(x_p, t^n)$과 동일하고, $x_p$는 grid point $x_{i-1}, x_i$ 사이에 위치함. $x_p$의 값은 두 개의 grid point $(x_{i-1}, u^n_{i-1})$와 $ (x_{i}, u^n_{i}) $를 활용하여 linear interpolation function $\tilde{u}(x)$를 수행하여 추정할 수 있음.
- $x_p$와 $x_i$간의 distance $d$는 $d=\Delta ta = \Delta t a / \Delta x \cdot \Delta x = c \Delta x$이기 때문에 $x_p=(i-1)\Delta x + (1-c)\Delta x$ 로 표현할 수 있음.
- Linear interpolation function은 다음과 같으며, $x=x_p$를 대입하면 해당 식은 first-order upwind scheme과 정확하게 같아짐. $$ \tilde{u}(x) = u^n_{i-1} + \frac{(u^n_i - u^n_{i-1})}{\Delta x} (x - x_{i-1})$$
- 위의 그림을 통해서, stability condition을 만족하려면 grid speed $\Delta x / \Delta t$가 wave speed $a$보다 커야하며, 이는 numerical domain of dependence가 PDE의 true domain of dependence를 포함시켜야 된다는 것을 의미함.
- *Truncation error 분석을 통해서 CIR scheme이 공간과 시간에 대해서 first-order accurate함을 확인할 수 있음. CIR scheme에 해당하는 modified equation은 아래와 같으며, $\alpha_\text{cir}$ 는 CIR scheme의 numerical viscosity coefficient임. 이로 인해, scheme의 artificial 또는 numerical viscosity가 생김. $$ q_t + aq_x = \alpha_\text{cir}q_xx $$ $$ \alpha_\text{cir} = \frac{1}{2}\Delta x a (1-|c|) $$
- $\Delta x=0$일 때 numerical viscosity는 사라지지만, $\Delta x =0$을 적용하는 것은 불가능함.
- $|c| = 1$일 때도 제거되지만, non-linear system에서 CFL을 1로 정하는 것은 불가능함.
- 일반적으로 $\alpha_\text{cir}>0$이기 때문에, solution의 discontinuities는 심하게 spread되거나 smeared 되고, extreme values는 clipped됨. 이는 first-order method인 CIR scheme의 단점임.
- CIR scheme의 general form을 아래와 같은 형태로도 표현할 수 있는 데, CFL stability condition을 만족하기 위해서 모든 cofficient는 0보다 크거나 같아야함. $$ u^{n+1}_i = H\left( u^n_{i-l_L}, ..., u^n_{i+l_R} \right) = \sum^{l_R}_{k=-l_L} b_ku^n_{i+k} $$ $$ b_{-1} = c^+, \quad b_{0} = (1-|c|), \quad b_1 = -c^{-} $$
Def. Monotone Schemes
- 모든 coefficient $b_k$가 0보다 크거나 같으면, 해당 scheme을 monotone하다고 함. 이는 function $H$로도 표현할 수 있음. $$ \frac{\partial H}{\partial u^n_k} \ge 0, \forall k $$
- Monotone scheme은 최대 first-order accurate만을 가질 수 있음.
Well-Known Schemes
Lax and Friedrichs (LF) Scheme
- LF scheme도 first-order scheme이지만, CIR scheme과는 다르게 upwind direction에 따라 차분할 필요가 없음. 이는 $u^n_i = 0.5(u^n_{i-1} + u^n_{i+1})$를 적용하여 구할 수 있음. $$ u^{n+1}_i = \frac{1}{2}(1+c)u^n_{i-1} + \frac{1}{2}(1-c)u^n_{i+1} $$
- von Neumann stability 분석을 통해, CFL condition이 $0 \le |c| \le 1$일 때 stable하다는 것을 알 수 있고, truncation error 분석을 통해서 해당 scheme이 first-order accurate임을 확인할 수 있음. LF scheme의 modified euqation은 다음과 같음. $$ q_t + aq_x = \alpha_\text{lf}q_xx $$ $$ \alpha_\text{lf} = \frac{ \Delta x a }{2c} (1-c^2) $$
- CIR scheme과의 numerical viscosity coefficient 비교를 통해, LF scheme이 더 많이 diffusive하다는 것을 알 수 있음. $$ 2 \le \frac{\alpha_\text{lf}}{\alpha_\text{cir}} = \frac{1+c}{c} < \infty $$
- LF scheme을 function $H$로 표현하면, 모든 coefficient $b_k$가 0보다 크거나 같기 때문에 LF scheme은 monotone함. $$ b_{-1} = \frac{1}{2}(1+c), \quad b_0 = 0, \quad b_{1} = \frac{1}{2}(1-c) $$
Lax and Wendroff (LW) Scheme
- LW scheme은 time derivative에 대해서 first-order forward approximation을 적용하고, space derivative에 대해서는 아래와 같이 upwind과 downwind approximations을 average함. $$ u_x = \beta_1\frac{u^n_i - u^n_{i-1}}{\Delta x} + \beta_2\frac{u^n_{i+1} - u^n_i}{\Delta x} $$ $$ \beta_1 = \frac{1}{2}(1+c), \quad \beta_2 = \frac{1}{2}(1-c) $$ $$ u^{n+1}_i = \frac{1}{2}c(1+c)u^n_{i-1} + (1-c^2)u^n_i - \frac{1}{2}c(1-c)u^n_{i+1} $$
- 유도하기 위해 적용한 approximation이 first-order accurate이지만, LW scheme은 space와 time domain에서 second-order임. 이를 통해서, scheme의 order of accuracy는 일반적으로 partial derivative에 대한 finite difference approximation의 order of accuracy로부터 추론할 수 없음.
- 또한, spatial derivative을 위해 사용한 approximation이 unconditionally unstable scheme이지만, LW scheme은 conditionally stable함.
- LW scheme을 function $H$ 형태로 표현하였을 때, 모든 coefficient가 0보다 크거나 같은 것이 아니기 때문에 LW scheme은 monotone하지 않음. $$ b_{-1} = \frac{(1+c)c}{2}, \quad b_0 = 1-c^2, \quad b_{1} = -\frac{(1-c)c}{2} $$
- Scheme이 monotone 하지 않다는 것은 discontinuity와 같은 sharp gradient가 존재하는 영역의 numerical solution에서 spurious oscillation 현상이 발생한다는 것을 의미함.
Warming and Beam (WB) Scheme
- WB scheme은 second-order accurate, upwind scheme임. $a$가 positivie일 때, 다음과 같은 식으로 표현할 수 있는데, stencil 중심을 제외한 모든 mesh point가 stencil 중심의 왼쪽에 위치하기 때문에 fully one-sided임. $$ u^{n+1}_i = \frac{1}{2}c(c-1)u^n_{i-2} + c(2-c)u^n_{i-1} + \frac{1}{2}(c-1)(c-2)u^n_i $$
- WB scheme은 not monotone하며, stability 조건은 $0 \le |c| \le 2$임. 넓어진 CFL stability 조건 범위로부터 더 큰 간격의 time step $\Delta t$을 사용할 수 있음.
Fromm Scheme
- Fromm scheme도 second-order scheme이며, $a$가 양수일 때 다음과 같이 표현할 수 있음. \[
\begin{aligned}
u^{n+1}_i = & -\frac{1}{4}(1-c)cu^n_{i-2} + \frac{1}{4}(5-c)cu^n_{i-1} \\
& + \frac{1}{4}(1-c)(4+c)u^n_i - \frac{1}{4}(1-c)cu^n_{i+1}
\end{aligned}
\] - Stability 조건은 $0 \le |c| \le 1$이며, 해당 scheme은 not monotone함.
- Lax-Wendroff, Warming-Beam, Fromm scheme과 같은 second-order scheme은 아래의 modified equation을 가지기 때문에 dispersive equation임. $$ q_t + aq_x = \beta q_{xxx} $$
Conservative Methods
- Shock wave와 같은 discontinuity를 포함하는 solution을 계산할 때는 conserved variable로 표현되는 formulation을 활용하는 데, non-conservative variable 기반의 formulation을 사용하면 wrong shock condition으로 인해 wrong shock strength, shock speed, shock position을 만들어냄.
Basic Definitions
- Conservative shock capturing method, especially upwind method의 기본 concept을 이해하기 위해 미분 형태로 표현된 scalar conservation law를 생각할 수 있음. $$u_t + f(u)_x = 0$$
- *Weak solution(↔ strong solution)이 포함되도록 적분 형태로 표현하면 아래와 같음. $$\oint(u dx - f dt) = 0$$ $$ \int^{x_2}_{x_1}u(x,t_2)dx = \int^{x_2}_{x_1}u(x,t_1)dx + \int^{t_2}_{t_1}f(u(x_1, t))dt - \int^{t_2}_{t_1}f(u(x_2, t))dt $$
* Weak solution: 충격파와 같은 불연속성이 포함된 문제에서
미분방정식으로는 정의될 수 없는 해가 존재함.
weak solution은 미분 연산이 정의되지 않을 때 적분 형태의 방정식을 만족하는 해를 의미함.
Def. Conservative Method
- Scalar conservation laws에 대한 conservative scheme은 아래와 같이 표현할 수 있는데, $f_{i+1/2}$는 numerical flux라고 하며 physical flux $f(u)$에 대한 approximation임. $$ u^{n+1}_i = u^n_i + \frac{\Delta t}{\Delta x}\left[ f_{i-1/2} - f_{i+1/2} \right] $$ $$ f_{i+1/2} = f_{i+1/2}(u^n_{i-l_L}, ..., u^n_{i+l_R} ) $$
- Numerical flux는 아래의 consistency condition을 충족해야 함. 이는 모든 argument가 $v$라면, numerical flux가 $u=v$에서의 physical flux와 동일하다는 것을 의미함. $$ f_{i+1/2}(v, ..., v) = f(v) $$
Finite Volume Method
- Conservative scheme을 적용하기 위해 domain을 discretisation하고 분할된 finite volume에서 정의된 cell average를 사용함.
- 길이 $L$을 가지는 spatial domain을 (computing) cells로 불리우는 $M$개의 finite volume으로 나눌 수 있으며, cell $I_i$에 대해서 $x$의 범위는 다음과 같음. $$ x_{i-1/2} = (i-1)\Delta x \le x \le i\Delta x = x_{i+1/2} $$
- 극단 값 $x_{i-1/2}$와 $x_{i+1/2}$은 numerical flux가 적용되어야 하는 intercell boundary의 위치를 정의함. 이를 통해서 cell size는 $ \Delta x = x_{i+1/2} - x_{i-1/2} = L / M $으로 표현할 수 있음.
- Cell $i$안에서 $u(x,t)$의 평균값, cell average는 고정된 시간 $t=t^n=n\Delta t$에서 다음과 같이 정의됨. $$ u^n_i = \frac{1}{\Delta x}\int^{x_{i+1/2}}_{x_{i-1/2}}u(x,t^n)dx $$
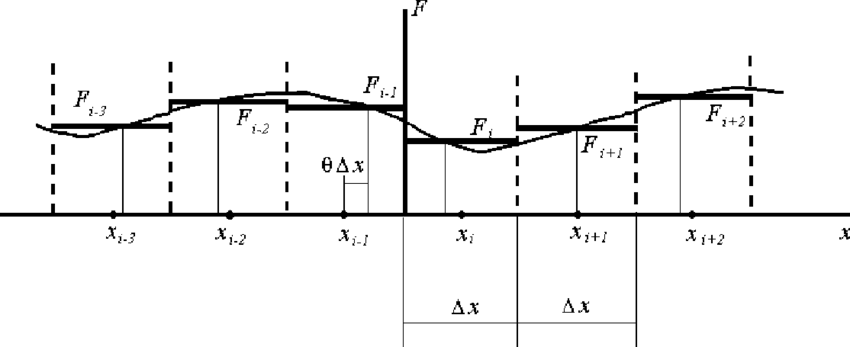
- 비록 cell $i$안에서 $u(x,t)$의 spatial variation이 존재하지만, integral average value $u^n_i$는 constant 값을 가짐. 해당 constant value를 cell 중앙에 할당하면 cell-centred conservative method가 됨.
- Cell averages들은 시간 $t_n$에서 piece-wise constant distribution을 정의함.