[Paper Review] Dataset Distillation by Matching Training Trajectories (MTT)

 

This is a Korean review of "Dataset Distillation by Matching Training Trajectories" presented at CVPR 2022.

 

TL;DR

• 합성데이터를 학습할 때, 모델의 파라미터가 실제 데이터로 학습했을 때의 파라미터 궤적과 유사한 경로를 따르도록 설계함.
• 이를 위해, 실제 데이터로 사전 학습된 전문가 네트워크의 학습 궤적(trajectory)을 미리 계산하고 저장함.

 

 

Introduction

• 기존 연구는 주로 낮은 해상도의 데이터셋 (e.g., MNIST, CIFAR)에만 국한되고, 다음의 한계가 존재함.
  • 여러 반복을 unroll하는 과정에서 학습 불안정성 발생
  • 막대한 연산 및 메모리 자원이 요구
  • 실제 데이터의 한 학습 스텝을 합성 데이터의 한 스텝으로 맞추는 방식을 사용하여, 평가 시 여러 스텝을 적용하면 오차가 누적
• 본 연구는 합성 데이터로 훈련된 파라미터 변화 궤적의 일부 구간을, 실제 데이터로 훈련된 전문가 궤적의 동일 구간과 일치시키도록 설계함. 이를 통해, 단기적인 스텝 매칭이나 전체 궤적 모델링과 같은 어려운 최적화 문제를 피할 수 있음.
  

  

  
  
  1. 실제 데이터로 여러 개의 모델을 학습하고 전문가 궤적을 저장
  2. 무작위로 선택한 전문가 궤적의 무작위 시점 파라미터로 모델을 초기화
  3. 해당 모델을 합성 데이터로 여러번 학습시킨 뒤, 전문가 궤적의 파라미터와 얼마나 일치하는 지를 손실로 계산하고, 역전파를 통해 합성데이터를 업데이트
• 해당 방법은 표준 데이터셋 (e.g., CIFAR-100, TinyImagenet)뿐만 아니라, 고해상도 데이터셋 (e.g., ImageNet)에도 적용 가능한 최초의 방법임.

 

 

Method

Expert Trajectories

• 합성 데이터로 훈련된 파라미터 $\hat{\theta}_t$ 궤적이 실제 데이터로 유도된 궤적 (i.e., *전문가 궤적 $\tau^*$)과 유사하도록 합성데이터를 만듦. 
• 전문가 궤적은 실제 데이터셋으로 여러 개의 네트워크를 학습시키고, 각 epoch 마다 파라미터를 저장하여 얻을 수 있으므로, 증류 전에 미리 계산해둘 수 있음.

*원본 데이터셋을 사용해 네트워크를 학습할 때 생성되는 파라미터의 시간적 순서 $\{\theta_t^*\}_{0}^{T}$를 의미

 

Long-Range Parameter Matching

• 각 증류 단계에서, 전문가 궤적의 임의 시점 파라미터 $\theta^*_t$를 샘플링하여 학생 파라미터를 초기화함 $\hat{\theta}_t = \theta_t^*$. 이때, 후반부 궤적은 파라미터 변화가 작아 유익한 신호가 적기 때문에, 최대 시점 $T^+$를 설정해 해당 시점 이후는 제외함.
• 합성 데이터 $\mathcal{D}_{\text{syn}}$를 활용해, 초기화된 학생 네트워크를 $N$번 gradient descent 업데이트 함.
  $$
  \hat{\theta}_{t+n+1} = \hat{\theta}_{t+n} - \alpha \nabla \ell(\mathcal{A}(\mathcal{D}_{\text{syn}}); \hat{\theta}_{t+n}),
  $$
  
  • 여기서, $\mathcal{A}$는 이전 연구에서 사용된 *미분 가능한 augmentation 기법이고, $\alpha$는 학습가능한 learning rate임.
  • 역전파를 통해 합성 데이터에 손실을 전달해야 하므로 $\mathcal{A}$는 반드시 미분 가능해야함.
• 이후, 전문가 궤적에서 $t$ 시점으로부터 $M$ 스텝 이후의 파라미터 $\theta^*_{t+M}$를 가져와 학생 네트워크의 업데이트된 파라미터 $\hat{\theta}_{t+N}$와 비교함. 이때, weight matching loss는 다음과 같이, normalized squared $L_2$임.
  $$
  \mathcal{L} = \frac{\left\| \hat{\theta}_{t+N} - \theta_{t+M}^* \right\|_2^2}{\left\| \theta_t^* - \theta_{t+M}^* \right\|_2^2}
  $$
  • Expert distance $ \theta_t^* - \theta_{t+M}^* $로 정규화함으로써, *궤적 후반부처럼 변화량이 적은 구간에서도 강한 신호를 얻을 수 있음.
  • 또한, 이 정규화는 neurons간 또는 layers간의 크기 차이도 *self-calibration하는 효과가 있음.
  • Cosine distance나 logit matching도 실험적으로 시도되었지만, $L_2$ 손실이 안정적이고 성능이 좋았음.
• 최종적으로, 이 손실 $\mathcal{L}$을 $N$개의 업데이트 과정 전체를 따라 역전파하여, 합성 이미지의 픽셀과 learning rate $\alpha$를 동시에 최적화함.
• 이때, 학습 가능한 $\alpha$를 최적화하는 것은, 학생과 전문가의 update 횟수 $(N, M)$를 고정해두고도, 학생의 학습 궤적이 전문가 궤적을 효과적으로 따라가도록 update 크기를 자동으로 조절하는 역할을 함.

*증류 과정에서는 실제 데이터가 전혀 사용되지 않고, 합성 데이터에만 증강을 적용하므로 Siamese augmentation은 필요 없음.
하지만, 전문가 궤적을 생성할 때 적용한 증강 기법과 일치시켜야 함.

 

*전문가 궤적의 변화가 거의 없으면 즉, $\theta_t^* - \theta_{t+M}^*$가 매우 작은 값을 가지기 때문에 학생 파라미터와 전문가 파라미터 간의 차이가 작더라도 (즉, 분자가 작더라도), 궤적 변화량 대비 상대 오차로 계산되기 때문에, 역전파 신호가 강해짐.

 

*각 레이어나 뉴런마다 파라미터 크기가 다르기 때문에 단순 $L_2$ 손실을 적용하면, 크기가 큰 레이어에 학습이 편항되게 됨. 전문가가 이동한 전체거리 $ \theta_t^* - \theta_{t+M}^* $는 파라미터 전체의 누적 변화량을 나타내므로, 이를 활용해 정규화를 하면, 큰 파라미터에 과도하게 편향되지 않음.

 

Memory Constraints

• 각 최적화 단계마다 모든 클래스의 모든 모든 이미지를 동시에 최적화해야 하므로, 합성 데이터셋의 크기가 커질수록 메모리 소비가 심각한 문제가 됨.
• 이전 방법들은 한 번에 하나의 클래스만 증류하여 메모리 사용을 줄였지만, trajectory matching에서는 전문가 궤적이 다중 클래스를 동시에 학습한 모델에서 생성되므로, 클래스별 증류 전략이 적절하지 않음.
• 각 distillation step마다 새로운 mini-batch를 샘플링하여 (outer loop, Algorithm 1 Line 3) 최적화하면 메모리 부담을 줄일 수는 있으나, 중복된 정보가 여러 합성 이미지에 증류되어, 합성 이미지들이 유사해지는 catastrophic mode collapse가 발생할 수 있음.
• 대신, 학생 네트워크의 각 업데이트마다 (inner loop, Algorithm 1 Line 10) 새로운 mini-batch $b$를 샘플링함. 이렇게 하면 최종 weight matching loss를 계산할 시점에는, 모든 합성 이미지가 한번 씩 학습에 사용되었을 것이 보장됨.

 

 

Experiments

Low-Resolution Data

• 클래스당 합성 이미지를 1장으로 제한하면, 클래스를 구별할 수 있는 모든 정보를 단 1장의 샘플에 압축시켜야 함. 반면, 더 많은 이미지를 허용하면, 클래스를 구별하는 특징들을 여러 이미지에 나누어 분산시킬수 있음.

Cross-Architecture Generalization

 

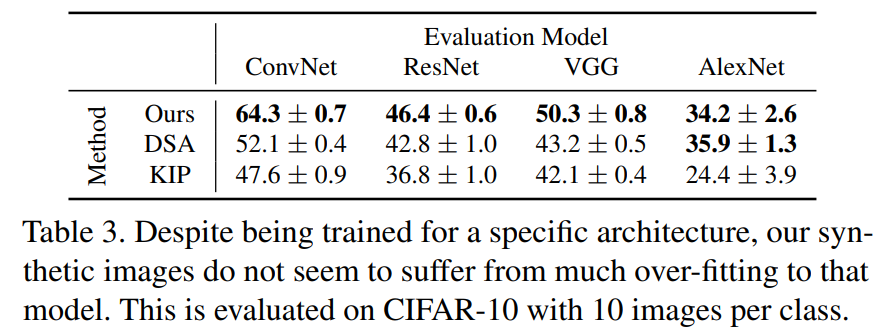
Short-Range vs. Long-Range Matching

• Short-range matching (e.g., $N = 1$ 및 작은 $M$)은 일반적으로 long-range matching보다 낮은 성능을 보임.
• Short-range matching 기반 방법인 DSA는 short-range behavior을 맞추는 데 최적화되어 있어, 학습이 길어질수록 오차가 누적되어 성능이 저하됨.

 

Tiny ImageNet

• Distribution Matching (DM)외의 대부분의 Dataset Distillation 방법들은 메모리 및 시간 소모가 매우 커서 큰 해상도에서는 제대로 작동하지 못함. 반면, 제안 방법은 뛰어난 성능을 보여줌.

 

ImageNet Subsets

• Tiny ImageNet 실험과 유사하게, 대부분의 기존 기법들은 이 정도 해상도에 적용하기 어려움. 따라서, 비교 대상으로 전체 real dataset으로 학습된 네트워크를 사용함. 

 

 

Discussion and Limitations

• 제안한 방법은 short-range single-step matching에 의존하지 않으며, 그렇다고 전체 학습 과정을 직접 최적화하는 full-process 방식에도 의존하지 않음. 오히려 두 접근법 사이의 균형을 잡는 전략을 통해, 안정성과 성능 면에서 기존 방법들을 모두 능가함.
• 본 방법은 $128 \times 128$ 해상도의 ImageNet 이미지에 확장된 최초의 증류 기법임.
• 제안한 방식은 expert trajectories을 사전 계산하여 메모리 사용량을 줄일 수 있는 장점이 있지만, 동시에 전문가 모델 학습과 궤적 저장을 위한 디스크 공간 및 계산 비용이 요구된다는 한계점이 존재함.