[Paper Review] Exploiting Inter-sample and Inter-feature Relations in Dataset Distillation

This is a Korean review of

"Exploiting Inter-sample and Inter-feature Relations in Dataset Distillation"
presented at CVPR 2024.

TL;DR

• 기존 dataset distillation 기법 중 하나인, distribution matching-based distillation은 두 가지 주요 문제를 가지고 있음.
  1. 동일한 클래스 안에서의 dispersed feature distribution으로 인해 낮은 class discrimination를 가짐.
  2.  Mean feature consistency에 대한 exclusive focus로 인해 부족한 precision과 comprehensiveness를 가짐.
• 이를 해결하기 위해, class centralization constraint를 적용하여 클래스 안의 sample들을 가깝게 clustering 하여 class discrimination을 향상함.
• 추가적으로, covariance matching constraint를 제안하여 local feature covariance matrix를 통해서 real과 synthetic dataset 간의 feature distribution matching를 향상함.

 

 

Introduction

• Dataset distillation은 neural architectur esearch [here], continual learning [here], privacy protection [here]과 같은 분야에서도 사용되는 기술임.
• 초기 dataset distillation은 전체 dataset으로부터 representative sample을 선택하는 coreset seletion method를 사용했지만, 이는 large dataset에서의 performance와 scalability의 한계가 존재함.
• Dataset distillation은 gradient matching, trajectory matching, distribution matching로 분류할 수 있음. Gradient matching과 trajectory matching은 second-order gradient optimization에 의존하기 때문에 computationally expensive 한 반면, distribution matching은 embedding space에서 feature distribution을 matching 함으로써 computational cost를 줄임.
• 하지만, distribution matching $($DM$)$는 두 가지의 중요 한계가 존재함.
  1. Synthetic dataset 안 동일 클래스에서의 sample feature distribution이 과도하게 분산되어 있고, 이는 embedding space에서 낮은 class discrimination을 초래함. 이는 작은 IPC에서 더욱 두드러짐.
  2. 기존 방법들은 real과 synthetic dataset 간의 mean feature에만 집중하기 때문에 feature distribution을 mathcing 하는 것이 부적절함.
• 이를 극복하기 위해 다음의 방법들을 제안함.
  1. Class centralization constraint를 통해 class-specific sample의 clustering을 향상함.
  2. 종합적인 feature distribution을 묘사하기 위해서는 means뿐만 아니라 covariance matrix $($inter-feature relationship$)$를 포함시켜야 하기 때문에 covariance matching constraint를 적용함.
     • 일반적으로 synthetic dataset은 sample의 개수가 feature dimension보다 적기 때문에 정확하게 covariance matrix를 예측하는 것이 어려움. 따라서, local feature covariance matrix를 통해 정확하게 feature distribution을 matching 함.

 

 

Related Works

Coreset selection

• Coreset selection은 dataset으로부터 representative sample을 고르는 방법으로, 가장 간단한 방법은 random selection이고, more sophisticate 한 Herding은 class center를 focus 함.
• 더 나아가, K-Center는 multiple centroid를 선택하고, Forgetting 방법은 학습 중 쉽게 잊어버리는 sample을 확인하여 representive sample를 고르는 방법임.

 

Dataset distillation

• Dataset distillation은 neural architecture search, continual learning, privacy protection 등의 application에서 활용됨. 
• 기존의 distribution matching method는 두 가지의 한계를 가지고 있음.
  1. Synthetic dataset의 동일 class안에서 dispersed feature distribution는 class discrimination을 줄임.
  2. Mean feature consistency에 exclusive focus 하여 precision와 comprehensiveness가 부족함.
• 이를 극복하기 위해, 본 논문은 두 개의 constraints를 제안하여 inter-sample과 inter-feature relations에 집중함.

 

 

Method

Preliminaries

• Dataset distillation의 목표는 smaller synthetic dataset $\mathcal{S}$으로 학습된 model $\psi_{\theta^\mathcal{S}}$이 large dataset $\mathcal{T}$으로 학습된 model $\psi_{\theta^\mathcal{T}}$에 상응하는 성능을 얻도록 하는 것임. 이는 아래의 objective function을 통해 최적화함.

\[
\underset{\mathcal{S}}{\mathrm{argmin}} \, \mathbb{E}_{x \sim P_{\mathcal{T}}} \| \ell (\psi_{\theta^\mathcal{T}}(\mathbf{x}), y) - (\psi_{\theta^\mathcal{S}}(\mathbf{x}), y) \|
\]

• DM은 대표적인 matching-based dataset distillation 방법이며, 이는 maximum mean discrepancy $($MMD$)$를 최소화하는 아래의 objective function을 사용함.

\[
\mathbb{E}_{\theta \sim P_{\theta}} 
\left\| 
\frac{1}{|\mathcal{T}|} \sum_{i=1}^{|\mathcal{T}|} \psi_{\theta} (\mathbf{x}_i) 
- \frac{1}{|\mathcal{S}|} \sum_{j=1}^{|\mathcal{S}|} \psi_{\theta} (\mathbf{s}_j)
\right\|^2
\]

 

Class centralization constraint $($inter-sample$)$

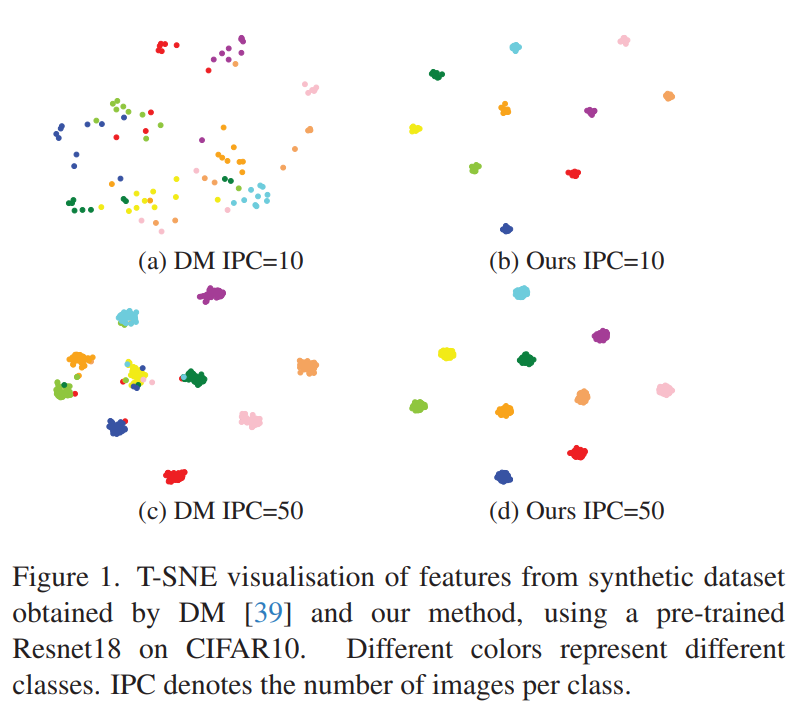
• Matching-based dataset distillation으로 얻어진 synthetic dataset은 class discrimination이 부족하며, IPC가 작을 때 더욱 두드러짐. 그림 1의 a와 c에서 볼 수 있는 것처럼, scattered feature distribution와 unclear class boundaries가 나타남.
• 이를 해결하기 위해, 아래의 class centralization constraint를 제안하여 동일 class안의 synthetic dataset로부터 추출된 feature $\phi(s)$를 cluster 하도록 함.

$$ \mathcal{L}_\text{CC} = \sum^C_c \left(\sum^K_{j=1}\max\left( 0, \exp \left( \alpha \| \psi(\mathbf{s}^c_j) - \bar{\psi}(\mathbf{s}^c) \|^2 \right) - \beta \right) \right), $$

$$ \bar{\psi}(\mathbf{s}^c) = \frac{1}{K}\sum^K_{j=1}\psi(\mathbf{s}^c_j) $$

• $\beta$는 centralization threshold이며, 작은 값일수록 each class안에서 샘플의 tighter clustering을 할 수 있음.
• 이 방법은 plug-and-play constraint이기 때문에 DM에서 사용하는 original constraint도 그대로 사용함. DM의 constraint에서는 model $\psi$로 randomly parameter-initialized ConvNet을 사용했지만, class centralization constraint에서는 Resnet18을 model로 사용함.
• 이를 통해, class feature를 효과적으로 구별할 수 있고, 서로 다른 neural network를 사용했기에 cross-architecture generalization을 향상할 수 있음.

 

Covariance matching constraint $($inter-feature$)$

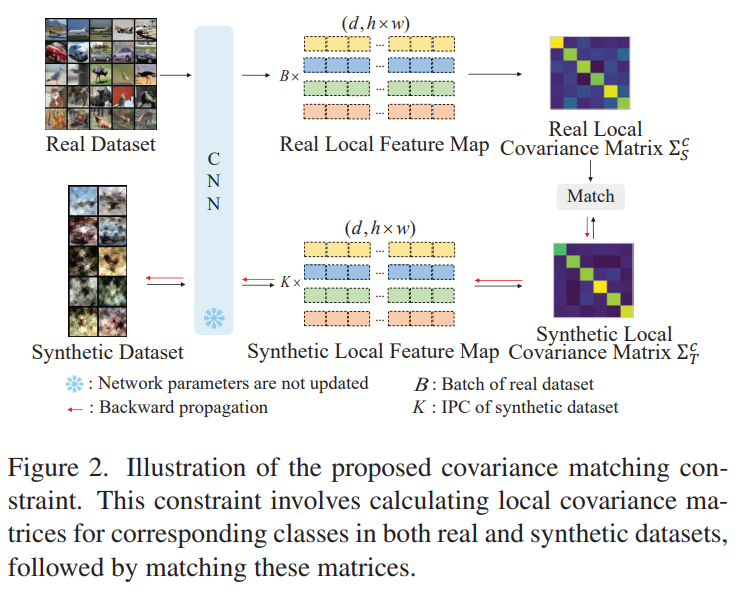
• Distribution matching-based dataset distillation는 real과 synthetic dataset의 feature distribution을 align 하는 것을 목표로 하지만, 주로 feature means matching에 focus 되어 있음. 
• 효과적인 representation을 위해서는 inter-feature relationship을 포착하는 covariance matrix를 고려해야 함. 하지만, distilled synthetic dataset의 경우, 각 class의 sample 수가 feature dimension보다 훨씬 작은 small sample problem이 발생하기 때문에 부정확한 covariance matrix estimation를 초래함.
• 이를 해결하기 위해, sample size가 feature dimension보다 훨씬 적은 상황에서도 정확한 matching 할 수 있는 covariance matching constraint를 제안함.
• 이는 single sample의 feature를 위해 flattening 하는 대신, $(d, hw)$의 tensor로 reshape 하여, real dataset에 대한 $ X_i \in \mathbb{R}^{d \times hw} $와 synthetic dataset에 대한 $ S_i \in \mathbb{R}^{d \times hw} $으로 표현되는 $d hw$-dimensional local feature descriptors를 얻음. 이를 통해, feature dimension을 크게 줄여, high-dimensional vector space computation을 피할 수 있음.
• Local feature descriptor를 활용해 local feature covariance matrix $\Sigma_\tau\in \mathbb{R}^{d\times d}$를 계산하고 two matrices 사이의 matching loss를 계산할 수 있음.

$$ \mathcal{L}_\text{CM} = \sum^C_{c=1}\| \Sigma^c_s - \Sigma^c_\tau \|^2, $$

$$ \Sigma^c_s =\frac{1}{K}\sum^K_{i=1}(S^c_i - \bar{S}^c) (S^c_i - \bar{S}^c)^\text{T},  $$

$$ \Sigma^c_\tau = \frac{1}{B} \sum_{i=1}^B (X^c_i - \bar{X}^c)(X^c_i - \bar{X}^c)^\text{T}. $$

 

Objective function

• 제안한 constraints는 plug-and-play이기 때문에 다양한 distribution matching-based method에 적용가능함. DM과 IDM을 baseline method로 활용하면, 아래의 objective function으로 표현할 수 있음.

$$ \mathcal{L} = \mathcal{L}_\text{DM} + \lambda_\text{CC}\mathcal{L}_\text{CC} + \lambda_\text{CM}\mathcal{L}_\text{CM} $$

\[
\mathcal{L} = \mathcal{L}_\text{IDM} + \lambda_\text{CC}\mathcal{L}_\text{CC} + \lambda_\text{CM}\mathcal{L}_\text{CM}
\]

 

 

Experiments

Network architectures: method section에서 언급한 것처럼, 최종 objective function에서 $\mathcal{L}_\text{DM}$과 $\mathcal{L}_\text{IDM}$를 위해서는 ConvNet을 사용하고, class centralization constraint $\mathcal{L}_\text{CC}$를 위해서는 30 epoch동안 학습시킨 ResNet18을 활용함.

 

Comparison with SOTA methods

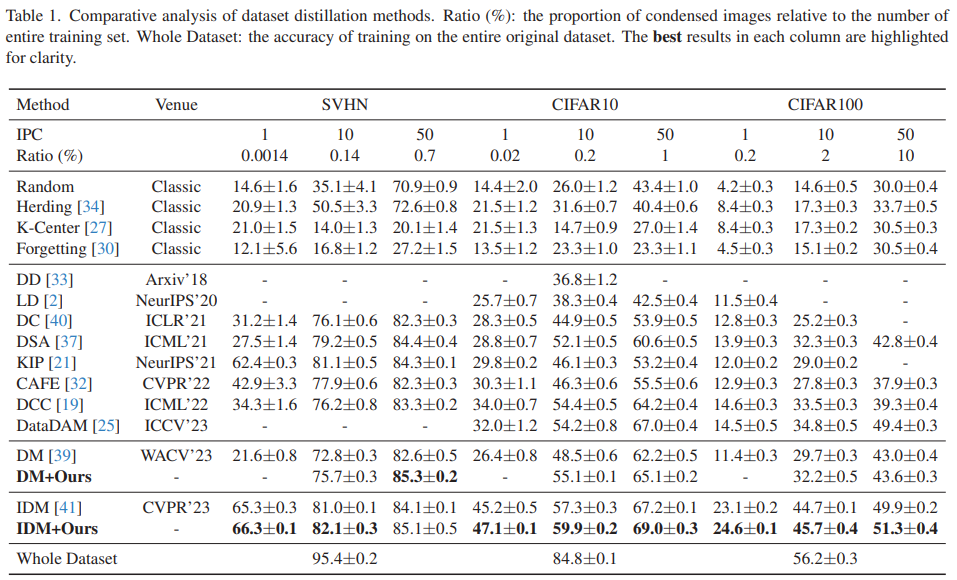
• DM+Ours의 결과가 IPC=1인 경우에 누락되어 있는데, 이는 1보다 큰 sample size가 필요하기 때문임. 다만, IDM+Ours의 결과는 IPC=1인 경우에도 존재하는데, IDM은 partitioning과 expansion augmentation을 통해서 IPC=1에서도 더 많은 sample을 보유할 수 있기 때문임.

 

Cross-architecture generalization

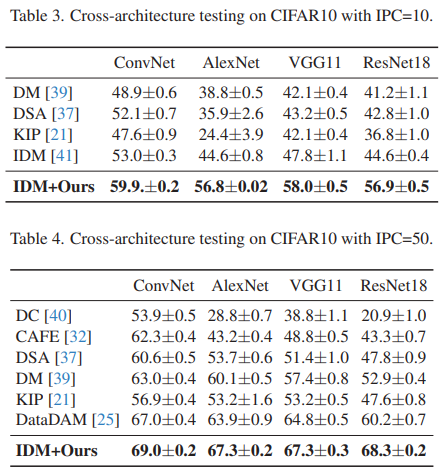
• Cross-architecture generalization은 dataset distillation을 평가하는 중요 지표인데, real appliation에서 사용될 neural network architecture를 예측하는 것이 어렵기 때문임.

 

Abliation study

Analysis of cluster constraint threshold

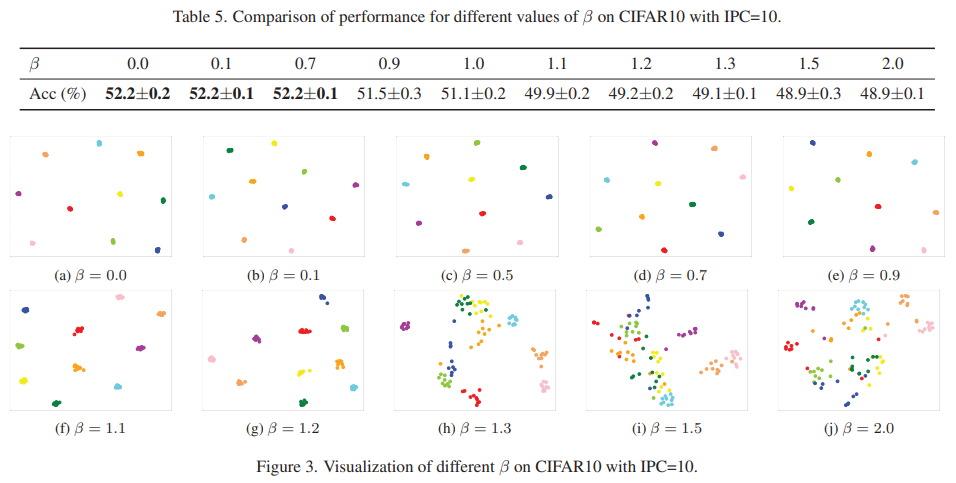
• $\beta$는 centralization threshold이며, 큰 $\beta$는 sample feature가 class feature center로부터 멀어지도록 하고, $($dispersed feature distribution$)$ 작은 $\beta$는 가까워지도록 함 $($concentrated feature distribution$)$. 이는 그림 3을 통해서도 확인할 수 있음.
• 본 실험을 통해, 작은 $\beta$가 higher class discrimination을 얻도록 함을 알 수 있음.

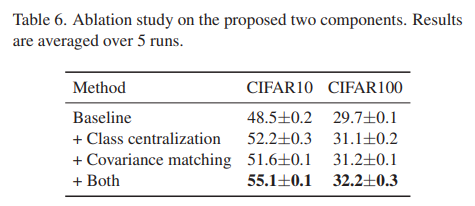
Effectiveness of each component

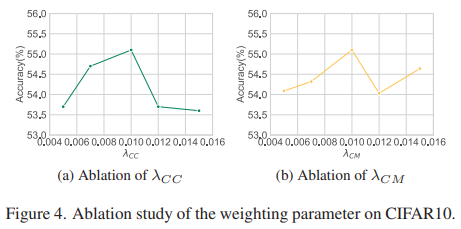
Evaluation of weighing parameter

Number of iterations required for convergence

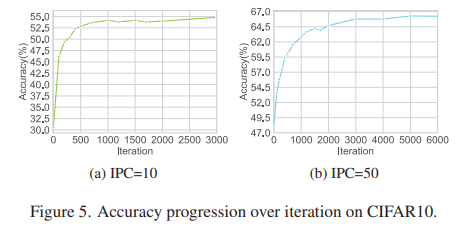
• 이전 방법들이 20,000번의 iteration이 필요한 것과 반대로, 제안 방법은 매우 적은 iteration에서도 수렴하였음. 또한, training의 초기 단계에서 성능이 빠르게 증가하기 때문에, 자원이 제한적일때 early stopping training method를 고려할 수 있음.

Different compression ratios

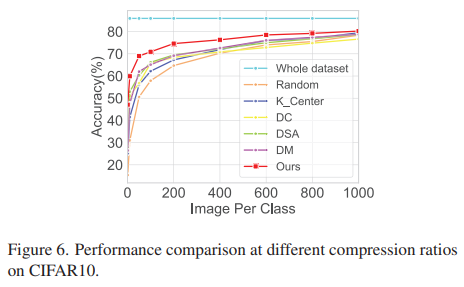
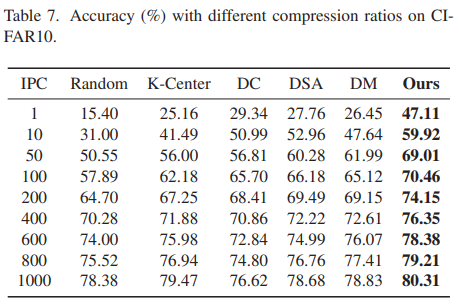
• 매우 작은 compression ratio에서 성능을 증가시키는 것도 중요하지만, 전체 dataset과 유사한 성능을 얻기 위해 필요한 compression ratio를 결정하는 것도 중요함.
• 제안 방법이 다양한 IPC에서 타 방법 대비 뛰어난 성능을 기록하지만, compression ratio가 증가할수록 performance gap이 줄어듦. 즉, 제안 방법은 smaller compression ratio에서 더욱 효과적임.
• 성능과 data reduction간의 최적 balance를 위해 큰 compression ratio에서 적절한 dataset distillation을 연구하는 것이 의미 있을 것으로 생각됨.

 

Applications

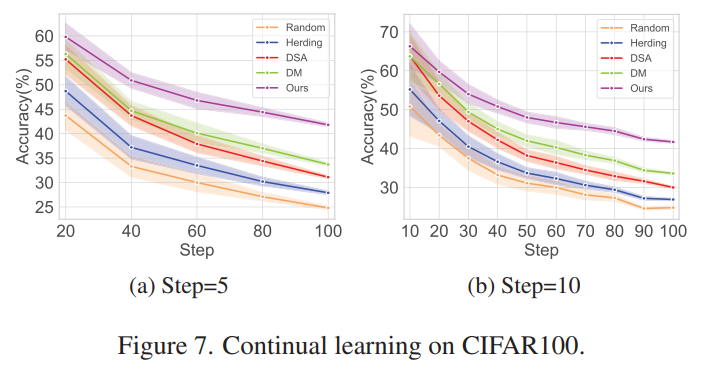
Continual learning: 이전에 학습했던 task를 잊는 것을 최소화하되, 새로운 task에 적응할 수 있는 model을 개발하는 방법으로, dataset distillation은 continual learning에서 활용될 수 있음.

 

Visulization

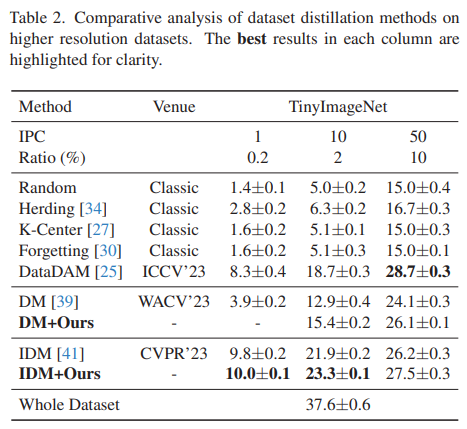
• SVHN, CIFAR10/100과 같은 smaller resolution dataset에서는 대부분의 high-frequency information이 보존되기 때문에 human eye로도 잘 인식되지만, TinyImageNet과 같은 higher resolution dataset의 경우, real dataset과 꽤 달라져 시각적으로 구별하기 어려워짐.

 

 

Conclusion

• 이전의 distribution matching-based method는 불충분한 class discrimination과 불완전한 distribution matching의 주요 한계가 있었기 때문에, 이를 극복하고자, ① class centralization constraint를 통해 class center에 가깝게 sample을 clustering 하여 inter-sample을 향상했으며, ② covariance matching constraint를 통해 inter-feature relationship을 향상함.