This is a Korean review of
"Scale Decoupled Distillation"
presented at CVPR 2024.
TL;DR
- 기존 logit-based KD는 multiple semantic knowledge가 couple 되어 있는 global logit ouput을 활용하기 때문에 ambigous knowledge를 전달하며, sub-optimal 함.
- Scale Decoupled Distillation $($SDD$)$ 를 통해 global logit을 multiple local logit으로 분리하여, fine-grained 하고 unambiguous logit을 전달하도록 함.
- 더 나아가, decoupled knowledge를 consistent logit과 complementary logit로 나눠 각각 semantic information과 sample ambiguity를 전달함. 여기에, complementary logit의 weight를 증가시켜 ambiguous sample에 더 집중하도록 함.
Introduction

- Logit-based KD는 크게 두 개의 그룹으로 나눌 수 있음. 하나의 그룹은 multiple classifiers 또는 self-supervision learning를 통해 풍부한 logit knowledge를 추출하는 방법이고, 또 다른 그룹은 dynamic temperature 또는 knowledge decoupling을 통해 knowledge transfer를 최적화하는 방법임.
- 하지만, 모두 global logit knowledge에 의존하기 때문에 sub-optimal 한 결과를 도출함.
- 이미지는 일반적으로 여러 개의 class에 대한 정보가 couple 되어 있으며, 비슷한 superclass에 속하는 class들은 유사한 global information을 공유함. 즉, global logit output은 다양한 fine-grained semantic knowledge가 혼합되어 있고, 이는 ambiguous knowlege를 전달해 sub-optimal 성능을 얻게 함.
- 본 논문은 SDD를 제안하여, whole image의 logit output을 multiple local region의 logit output으로 decouple 함. 이를 통해, 풍부하고 unambiguous semantic knowlege를 얻을 수 있음.
- 더 나아가, decoupled logit output을 consistent term$($global logit output과 동일한 class$)$과 complementary term $($global logit output과 다른 class$)$ 으로 분리하여, 각각 multi-scale knowledge를 전달하고 sample ambiguity를 보존하도록 함.
Related Work
Feature-based Distillation
Logit-based Distillation
Method

Notation
- Teacher와 student network를 penultimate layer의 feature map $R^{c_{Net}\times h_{Net}\times w_{Net}}$을 얻을 수 있는 convolutional feature extractor $f_{Net}$과 이러한 feature vector를 $K$개의 class logit $z^l_{Net}$으로 projection 하는 projection matrix $W_{Net}$로 나눌 수 있음.
- Location $(j, k)$에서의 feature vector는 $f_{Net}(j, k)=f_{Net}(x)(:, j, k)\in R^{c_{Net}\times 1\times 1}$로 나타낼 수 있음.
Conventional Knowledge Distillation
- 기존의 logit기반 KD방법들은 아래의 loss를 통해 knowledge를 distillation 하게 됨.
\[ \begin{aligned} & L_\text{KD} = \mathcal{K}\mathcal{L}(\sigma(P_T) \| \sigma(P_S)) \\
& P_T = W_T \sum_{j=0}^{h_T-1} \sum_{k=0}^{w_T-1} \frac{1}{h_T w_T} f_T(j, k) \\
& P_S = W_S \sum_{j=0}^{h_S-1} \sum_{k=0}^{w_S-1} \frac{1}{h_S w_S} f_S(j, k) \end{aligned} \]
- 해당 식에서 fully connected layer $W_{Net}$의 선형성으로부터 $L_{Net} = W_{Net}f_{Net}(x)$를 적용하면, 다음과 쓸 수 있음.
\[ \begin{aligned} P_T &= \sum_{j=0}^{h_T-1} \sum_{k=0}^{w_T-1} \frac{1}{h_T w_T} L_T(j, k), \\ P_S &= \sum_{j=0}^{h_S-1} \sum_{k=0}^{w_S-1} \frac{1}{h_S w_S} L_S(j, k). \end{aligned} \]
- 이를 통해, conventional logit-based distillation은, 서로 다른 위치의 local feature vector로부터 계산된, 서로 다른 local logit knowledge가 혼합된 average logit output을 활용한다는 것을 알 수 있음.
- 하지만, 그림 1을 통해 알 수 있듯, 서로 다른 local output은 일반적으로 서로 다른 sematic inforamation을 포함하며, logit output에 단순하게 합치는 것은 ambiguous knowledge를 student에게 전달하도록 하고, sub-optimal performance를 만들어 냄.
- 이를 위해, logit output을 scale level로 decouple 하여 더욱 풍부하고 unambiguous logit$($local과 golobal category가 일치$)$을 student에게 전달하도록 하는 SDD를 제안함.
Scale Decoupled Knowledge Distillation
- SDD는 multi-scale pooling과 information weighting의 두 개의 part로 이루어짐.
- Multi-scale pooling은 input image의 서로 다른 region에 대한 logit output을 얻기 위해, 서로 다른 scale에 대해서 average pooling을 적용하는 것이며, 이는 student가 clear semantic을 가지는 fine-grained knowledge를 보존하도록 도와줌.
- Information weighting은 global logit과 class가 일치하지 않는 local logit에 대한 loss weight를 증가시키는 것이며, 이를 통해 student를 local과 global category가 다른 ambiguous sample에 더욱 집중하도록 함.
Multi-scale pooling
- Multi-scale pooling은 logit output map을 다양한 scale의 cell로 분리하고, 각 cell에서의 logit knowledge를 aggregation 하기 위해 average pooling을 수행함.
- $m$-th scale에서 $n$-th 셀의 공간적 영역은 $\mathcal{C}(m, n)$으로, 이 cell에 해당하는 input region은 $\mathcal{Z}(m, n)$으로, 이 region에 대한 networks의 logit output $\pi_{Net}(m, n)\in R^{K\times 1\times 1}$는 아래와 같이 표현할 수 있으며, 이는 해당 cell에서의 aggregated logit knowledge를 의미함.
$$ \pi_{Net}(m, n) = \sum_{j,k\in \mathcal{C}(m, n)} \frac{1}{m^2}L_{Net}(j, k)$$
- 영역 $\mathcal{Z}(m, n)$에서의 logit knowledge를 전달하기 위한 distillation loss $\mathcal{D}(m, n)$은 아래와 같이 정의할 수 있음.
$$ \mathcal{D}(m, n)=\mathcal{LD}(\sigma (\pi_T(m, n)), \sigma (\pi_S(m, n)) ) $$
- 모든 scale $M=[1,2,4,...,w]$과 이에 대한 cells $N_m={1,4,16,...w^2}$에 대한 정보를 전달하기 위해 최종 SDD loss는 다음과 같이 정의됨.
$$ \mathcal{L}_\text{SDD} = \sum_{m\in M} \sum_{n\in N_m}\mathcal{D}(m, n) $$
Information weighting
- Decoupled logit output을 다시, global logit output과 같은 class에 속하는 consistent term과 다른 class에 속하는 complementary term으로 나눌 수 있음. Consistent term은 해당 class에 대한 multi-scale knowledge를 student에게 전달하고, complementary term은 student가 $($teacher와 동일하게$)$sample ambiguity를 유지하도록 함.
$$ \mathcal{L}_\text{SDD} = \mathcal{D}_\text{consistent} + \beta \mathcal{D}_\text{complementary} $$
- Global prediction이 옳고, local prediction이 틀린 경우의 complementary term은 student가 sample ambiguity를 유지하도록 해 stduent가 ambiguous sample에 지나치게 확신하지 않도록 하여 over-fitting을 방지함. 반면, global prediction이 틀리고, local prediction이 옳은 경우에는 ambiguity를 통해 student가 서로 다른 category 간의 유사한 component를 학습하도록 만들어 teacher로부터 야기되는 편향을 완화시키고 일반화된 지식을 학습하도록 함.
Compared with others
- $m=w_T=h_T, n=1$로 설정하면, SDD loss는 conventional distillation loss로 돌아가며, 이는 student가 global logit으로부터 contextual information을 배우도록 함. 반면, $m<w_T=h_T$로 설정하면, SDD는 fine-grained semantic knowledge를 유지하도록 하고, student가 teacher로부터 다양하고 명확한 semantic knowledge를 학습하도록 하여, ambiguous sample에 대해서 discrimination 능력을 향상시킴.
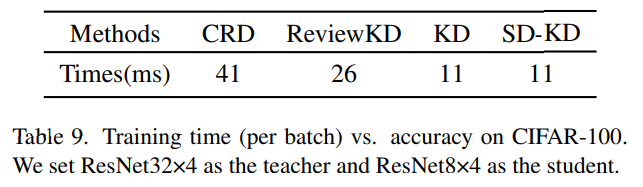
- 기존의 Multi-branch KD가 다수의 classifier를 사용하여, 추가적인 complexity을 수반하는 것과는 다르게, SDD는 여전히 하나의 classifier를 사용하여 multi-scale logit을 얻기 때문에 single-branch 방법이며, 추가적인 computational complexity가 없음 $($Table 9 참조$)$.
- DKD가 class scale에서 logit을 decouple 하고 logit output을 얻은 이후에 수행하는 것과는 반대로, SDD는 spatial scale에서 logit을 decouple 하며 logit output을 얻기 전에 수행함.
Experiment
Comparison Results





- 작은 discrepancy를 가지는 서로 다른 class가 존재하는 task $($i.e., fine-grained classification task$)$에서 더욱 뛰어난 성능을 기록함. 이는 fine-grained classification task가 fine-grained semantic information에 더욱 의존하기 때문이며, 동시에 SDD가 local information을 잘 포착하기 때문임.
Ablation Study


- Teacher-student가 heterogenous 구조일 때, 더 다양한 sclaes을 적용하는 것이 성능개선에 도움이 됨. 이는 heterogeneous 구조가 more fine-grained semantic knowledge가 필요하며, homogenous 구조의 경우, 너무 많은 scales에 대한 불필요한 정보를 활용하면 핵심 scale을 포착하는 것이 어렵기 때문임.

- $\beta$를 1보다 크게 설정할 때 높은 성능을 기록하는데, 이는 ambiguous sample에 더욱 집중하는 효과를 보여줌.
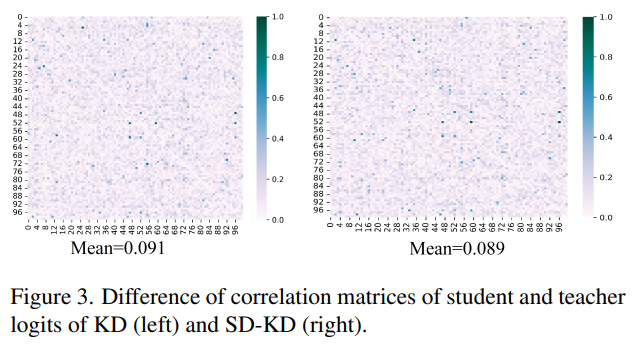
- DKD가 KD와 명확히 다른 corrrelation matrices를 얻는 것과 반대로, SD-KD는 KD와 유사한 결과를 보여주는데, 이는 SDD 성능 향상이 teacher의 global logit output을 더 잘 모방하는 것이 아니기 때문임.

- 그림 5를 통해, KD에 의해 잘못 예측된 sample은 global semantic이 유사하게 보이는 ambiguous sample임을 확인할 수 있음. 반면, SDD는 student가 local region의 fine-grained semantic information을 학습하도록 도와줘 올바르게 예측하도록 함.
Conclusion
- 기존의 global logit distillation의 coupled semantic knowledge transfer 한계를 밝히고, 이를 극복하기 위해 Scale-Decoupled Knowledge Distillation을 제안하여, global logit을 multiple local logit으로 decouple 하고, 더 나아가 이를 consistent와 complementary의 두 part로 나눠 student의 ambiguous sample에 대한 discrimination 능력을 향상시킴.