[Paper Review] Logit Standardization in Knowledge Distillation

This is a Korean review of

"Logit Standardization in Knowledge Distillation"
presented at CVPR 2024.

TL;DR

• KD에서 teacher와 student의 soft label $($i.e., prediction$)$을 얻을 때 사용하는 shared temperature은 teacher와 student logits의 range와 variance의 mandatory exact match를 전제로 함. $($in fact, relation is important.$)$
• 기존 방법의 한계를 극복하기 위해, adaptive temperature로 weighted logit standard deviation을 사용함.
• 이를 활용해, softmax를 적용하기 전, $\mathcal{Z}$-score pre-process를 수행함. 이를 통해 student가 magnitude match가 아닌 핵심적인 logit relation에 집중하도록 함.

Expression Transformation

	Student prediction
Convential Form $($including temperature $\mathcal{T})$	$$q{\left({\mathbf{z}}_n\right)}^{(k)}=\frac{\exp \left({\mathbf{z}}_n^{(k)}/\mathcal{T}\right)}{\sum _{m=1}^K\exp \left({\mathbf{z}}_n^{(m)}/\mathcal{T}\right)}$$
Constrained Entropy-Maximization Form $($with Lagrangian multipliers $\alpha ,\beta )$	$$q{\left({\mathbf{z}}_n\right)}^{(k)}=\frac{\exp \left({\beta }_n{\mathbf{z}}_n^{(k)}\right)}{\sum _{m=1}^K\exp \left({\beta }_n{\mathbf{z}}_n^{(m)}\right)}$$
General Form $($with hyper-parameters $a_S,b_S)$	$$q{({\mathbf{z}}_n;a_S,b_S)}^{(k)}=\frac{\exp \left[({\mathbf{z}}_n^{(k)}-a_S)/b_S\right]}{\sum _{m=1}^K\exp \left[({\mathbf{z}}_n^{(m)}-a_S)/b_S\right]}$$
Logit Standardization $($with mean ${\bar{\mathbf{z}}}_n$, weighted standard deviation $\sigma ({\mathbf{z}}_n))$	$$q{({\mathbf{z}}_n;{\bar{\mathbf{z}}}_n,\sigma ({\mathbf{z}}_n))}^{(k)}=\frac{\exp (\mathcal{Z}({\mathbf{z}}_n;\tau {)}^{(k)})}{\sum _{m=1}^K\exp (\mathcal{Z}({\mathbf{z}}_n;\tau {)}^{(m)})}$$

 

 

Introduction

• 본 논문은 classification과 KD에서 사용되는 softmax가 정보이론의 entropy maximization 원리에서 유도됨을 보이는데, 이 과정에서 temperature가 Lagrangian multiplier로부터 얻을 수 있음을 보임.
• 이를 바탕으로, teacher와 student의 temperature 간의 무관성$($irrelevance$)$뿐만 아니라, 서로 다른 sample의 temperature 간의 무관성을 규명하여, teacher와 student 간, 서로 다른 sample 간에 반드시 같은 temperature를 적용해야 할 필요가 없음을 보여줌.
• Teacher와의 capacity gap으로 인해 teacher와 유사한 range와 variance를 가지는 logit을 예측하는 것이 어려운데, 이를 극복하기 위해 adaptive temperature로서 weighted logit standard deviation을 사용하며, $\mathcal{Z}$-score logit standardization을 softmax 적용 전 pre-processing 단계로 제안함.
• $\mathcal{Z}$ pre-processing를 통해 logit의 arbitrary range를 bounded range로 mapping 하여 student logit이 teacher logit의 innate relationship을 보존하고 학습하도록 함.

 

 

Related Work

• 예측된 확률분포를 smooth 하게 만들기 위해 적용되는 temperature $\mathcal{T}$은 hyper-parameter로서 사전에 지정되어야 하며, 학습되는 동안 고정된 값을 가짐.
• CTKD는 adversarial learning을 적용해 sample 난이도에 따른 sample별 temperature를 활용했지만, teacher와 student가 동일한 temperature를 공유해야 한다고 가정함.
• ATKD [paper to read]가 sharpness metric을 제안하고, adaptive temperature를 적용했지만, zero logit mean이라는 ATKD의 가정은 numerial apporximiation에 의존함.
• 이전 연구를 통해, student와 teacher 간의 exact logits matcing 대신, prediction의 inter-class relation만으로도 충분하지만, 기존의 sharing temperature 적용은 여전히 implicit 하게 exact mathcing 하도록 만듦.

 

 

Background and Notation

• Student's logit은 ${\mathbf{z}}_n=f_s\left({\mathbf{x}}_n\right)$, teacher's logit은 ${\mathbf{v}}_n=f_t\left({\mathbf{x}}_n\right)$.
• Temperature $\mathcal{T}$가 포함된 일반적인 softmax function은 아래의 식으로 표현됨.

$$\begin{array}{rl}q{\left({\mathbf{z}}_n\right)}^{(k)}& =\frac{\exp \left({\mathbf{z}}_n^{(k)}/\mathcal{T}\right)}{\sum _{m=1}^K\exp \left({\mathbf{z}}_n^{(m)}/\mathcal{T}\right)},\\ q{\left({\mathbf{v}}_n\right)}^{(k)}& =\frac{\exp \left({\mathbf{v}}_n^{(k)}/\mathcal{T}\right)}{\sum _{m=1}^K\exp \left({\mathbf{v}}_n^{(m)}/\mathcal{T}\right)}.\end{array}$$

• Knowledge distillation은 아래의 KL divergence를 최소화하여 $q{\left({\mathbf{z}}_n\right)}^{(k)}$가 $q{\left({\mathbf{v}}_n\right)}^{(k)}$를 모방하도록 함.

$${\mathcal{L}}_{\mathrm{KL}}(q\left({\mathbf{v}}_n\right)\Vert q\left({\mathbf{z}}_n\right))=\sum _{k=1}^{K}q{\left({\mathbf{v}}_n\right)}^{(k)}\log \left(\frac{q{\left({\mathbf{v}}_n\right)}^{(k)}}{q{\left({\mathbf{z}}_n\right)}^{(k)}}\right)$$

• 이론적으로 $\mathit{z}$에 대해서만 optimization 할 때, cross-entropy loss와 동일함.
  → teacher prediction는 학습 동안에 고정된 값이고, student prediction을 최적화하는 과정이기 때문에, $\mathbf{v}$만을 포함하는 항을 상수로 간주하여 cross-entropy loss와 이론적으로 같다고 할 수 있음.

$${\mathcal{L}}_{\mathrm{CE}}(q\left({\mathbf{v}}_n\right)\Vert q\left({\mathbf{z}}_n\right))=-\sum _{k=1}^{K}q{\left({\mathbf{v}}_n\right)}^{(k)}\log q{\left({\mathbf{z}}_n\right)}^{(k)}$$

• $q\left({\mathbf{v}}_n\right)$의 negative entropy term로 인해 gradient가 diverge 하기 때문에 경험적으로는 같지 않음.
  → $\mathbf{v}$만을 포함하는 항이 상수지만, 해당 값으로 인해 loss의 값이 과도하게 커질 수 있기 때문에, 이로 인해 발생하는 하는 발산을 방지하기 위해 다른 방향으로 최적화과정이 진행돼서 cross-entropy loss와 다른 결과를 나타낸다는 뜻?

 

 

Method

• ${}^{1)}$Teacher와 student 간의, sample 간의 temperature irrelevance 및 ${}^{2)}$기존 shared temperature의 두 가지 단점을 언급하고, ${}^{3)}$temperature안의 factor로서 logit standard deviation를 적용한 logit standardization의 pre-process를 제안함.

1) Irrelevance between Temperatures

• KD와 classification에서의 temperature-involved softmax를 entropy-maximization principle를 통해 유도함. 이는 student와 teacher 간의, sample 간의 서로 다른 temperature 적용 가능성을 시사함.

Derivation of softmax in Classification

$$\underset{q}{max}{\mathcal{L}}_1=-\sum _{n=1}^N\sum _{k=1}^{K}q{\left({\mathbf{v}}_n\right)}^{(k)}\log q{\left({\mathbf{v}}_n\right)}^{(k)}$$

• 첫 번째 제한조건은 discrete probability density 조건으로, 확률 분포 정의에 따라 합이 1이 되어야 함.

$$\sum _{k=1}^{K}q{\left({\mathbf{v}}_n\right)}^{(k)}=1,\mathrm{\forall }n$$

• 두 번째 제한조건은 기댓값이 목표 클래스 $y_n$의 로짓 값과 일치하도록 하여, 모델이 정확하게 target class를 예측하도록 함.

$${\mathbb{E}}_q\left[{\mathbf{v}}_n\right]=\sum _{k=1}^K{\mathbf{v}}_n^{(k)}q{\left({\mathbf{v}}_n\right)}^{(k)}={\mathbf{v}}_n^{\left(y_n\right)},\mathrm{\forall }n.$$

• Lagrangian multipliers ${\alpha }_{1,n}$, ${\alpha }_{2,n}$를 적용하면 다음과 같이 식을 변형할 수 있음.

$$\begin{array}{rl}{\mathcal{L}}_T={\mathcal{L}}_1& +\sum _{n=1}^N{\alpha }_{1,n}(\sum _{k=1}^{K}q{\left({\mathbf{v}}_n\right)}^{(k)}-1)\\ & +\sum _{n=1}^N{\alpha }_{2,n}(\sum _{k=1}^K{\mathbf{v}}_n^{(k)}q{\left({\mathbf{v}}_n\right)}^{(k)}-{\mathbf{v}}_n^{\left(y_n\right)})\end{array}$$

• ${\alpha }_{1,n}$과 ${\alpha }_{2,n}$에 대해서 부분 미분하면 constraints로 돌아가고, $q{\left({\mathbf{v}}_n\right)}^{(k)}$에 대해 미분을 하면, 아래의 식으로 정리됨.

$$\frac{\partial {\mathcal{L}}_T}{\partial q{\left({\mathbf{v}}_n\right)}^{(k)}}=-1-\log q{\left({\mathbf{v}}_n\right)}^{(k)}+{\alpha }_{1,n}+{\alpha }_{2,n}{\mathbf{v}}_n^{(k)}$$

• 미분값에 0을 취하면 solution을 얻을 수 있음.

$$\begin{array}{c}q{\left({\mathbf{v}}_n\right)}^{(k)}=\exp \left({\alpha }_{2,n}{\mathbf{v}}_n^{(k)}\right)/Z_T\\ \text{ where }{Z}_T=\exp (1-{\alpha }_{1,n})=\sum _{m=1}^K\exp \left({\alpha }_{2,n}{\mathbf{v}}_n^{(m)}\right)\end{array}$$

Derviation of softmax in KD

• Constrained entropy-maximization optimization는 아래와 같음.

$$\underset{q}{max}{\mathcal{L}}_2=-\sum _{n=1}^N\sum _{k=1}^{K}q{\left({\mathbf{z}}_n\right)}^{(k)}\log q{\left({\mathbf{z}}_n\right)}^{(k)}$$

• 첫 번째와 두 번째 제한조건은 classification과 동일함.

$$\sum _{k=1}^{K}q{\left({\mathbf{z}}_n\right)}^{(k)}=1,\mathrm{\forall }n$$

$$\sum _{k=1}^K{\mathbf{z}}_n^{(k)}q{\left({\mathbf{z}}_n\right)}^{(k)}={\mathbf{z}}_n^{\left(y_n\right)},\mathrm{\forall }n$$

• 세 번째 제한조건은, KD에 의해 student가 완전히 학습되었다고 가정하면 teacher logit과 student logit이 동일해야 하기 때문에 추가됨.

$$\sum _{k=1}^K{\mathbf{z}}_n^{(k)}q{\left({\mathbf{z}}_n\right)}^{(k)}=\sum _{k=1}^K{\mathbf{z}}_n^{(k)}q{\left({\mathbf{v}}_n\right)}^{(k)},\mathrm{\forall }n.$$

• Lagrangian multipliers ${\beta }_{1,n}$, ${\beta }_{2,n},{\beta }_{3,n}$를 적용하면 다음과 같이 식을 변형할 수 있음.

$$\begin{array}{rl}{\mathcal{L}}_T={\mathcal{L}}_2& +\sum _{n=1}^N{\beta }_{1,n}(\sum _{k=1}^{K}q{\left({\mathbf{z}}_n\right)}^{(k)}-1)\\ & +\sum _{n=1}^N{\beta }_{2,n}(\sum _{k=1}^K{\mathbf{z}}_n^{(k)}q{\left({\mathbf{z}}_n\right)}^{(k)}-{\mathbf{z}}_n^{\left(y_n\right)})\\ & +\sum _{n=1}^N{\beta }_{3,n}\sum _{k=1}^K{\mathbf{z}}_n^{(k)}(q{\left({\mathbf{z}}_n\right)}^{(k)}-q{\left({\mathbf{v}}_n\right)}^{(k)})\end{array}$$

• $q{\left({\mathbf{z}}_n\right)}^{(k)}$에 대해 미분하고, ${\beta }_n={\beta }_{2,n}+{\beta }_{3,n}$로 정의하면 아래의 solution을 얻을 수 있음.

$$\frac{\partial {\mathcal{L}}_S}{\partial q({\mathbf{z}}_n{)}^{(k)}}=-1-\log q({\mathbf{z}}_n{)}^{(k)}+{\beta }_{1,n}+{\beta }_{2,n}{\mathbf{z}}_n^{(k)}+{\beta }_{3,n}{\mathbf{z}}_n^{(k)}$$

$$\begin{array}{c}q{\left({\mathbf{z}}_n\right)}^{(k)}=\exp \left({\beta }_n{\mathbf{z}}_n^{(k)}\right)/Z_S\\ \text{ where }{Z}_S=\exp (1-{\beta }_{1,n})=\sum _{m=1}^K\exp \left({\beta }_n{\mathbf{z}}_n^{(m)}\right)\end{array}$$

∴ Distinct Temperature

• 각 constraints는 $\alpha$ 또는 $\beta$와 관련이 없음. 따라서, ${\alpha }_{2,n}$와 ${\beta }_n$에 대한 explicit expression이 없으므로, manually 정의할 수 있음.
• ${\beta }_n={\alpha }_{2,n}=1/\mathcal{T}$로 정의하면, shared temperature를 적용하는 KD에서의 prediction으로 표현됨.
• ${\beta }_n={\alpha }_{2,n}=1$로 정의하면, 식은 classification에서 흔히 사용되는 전통적인 softmax function이 됨.
• 따라서, ${\beta }_n\ne {\alpha }_{2,n}$을 선택하면, student와 teacher에 서로 다른 온도를 적용할 수 있음.

∴ Sample-wisely different Temperature

• 일반적으로 모든 샘플에 대해서 global temperature를 정의하지만 $($i.e., any $n$에 대해서 ${\alpha }_{2,n},{\beta }_n$은 고정값으로 정의$)$, 이에 대한 제한조건이 없기 때문에 샘플에 따라 서로 다른 온도를 사용하는 것이 가능함.

 

2) Drawbacks of Shared Temperature

• Entropy-maximization으로부터 유도한 식을, hyper-parameters $a_S,b_S$를 추가해, general form으로 만들 수 있음. $($cf. $a_S=0,b_S=1/{\beta }_n$을 적용하면 원래대로 돌아감.$)$

$$\begin{array}{rl}q{\left({\mathbf{z}}_n\right)}^{(k)}& =\frac{\exp \left({\beta }_n{\mathbf{z}}_n^{(k)}\right)}{\sum _{m=1}^K\exp \left({\beta }_n{\mathbf{z}}_n^{(m)}\right)}\\ \to q{({\mathbf{z}}_n;a_S,b_S)}^{(k)}& =\frac{\exp \left[({\mathbf{z}}_n^{(k)}-a_S)/b_S\right]}{\sum _{m=1}^K\exp \left[({\mathbf{z}}_n^{(m)}-a_S)/b_S\right]}\end{array}$$

$$\begin{array}{rl}q{\left({\mathbf{v}}_n\right)}^{(k)}& =\frac{\exp \left({\alpha }_{2,n}{\mathbf{v}}_n^{(k)}\right)}{\sum _{m=1}^K\exp \left({\alpha }_{2,n}{\mathbf{v}}_n^{(m)}\right)}\\ \to q{({\mathbf{v}}_n;a_T,b_T)}^{(k)}& =\frac{\exp \left[({\mathbf{v}}_n^{(k)}-a_T)/b_T\right]}{\sum _{m=1}^K\exp \left[({\mathbf{v}}_n^{(m)}-a_T)/b_T\right]}\end{array}$$

• 이상적으로 학생이 완전한 정보를 전달받았다고 하면, KL divergence loss는 minimum에 도달하고, student의 확률분포는 teacher와 일치하게 됨. 즉, $\mathrm{\forall }k\in [1,K],q{({\mathbf{z}}_n;a_S,b_S)}^{(k)}=q{({\mathbf{v}}_n;a_T,b_T)}^{(k)}$ 따라서, arbitrary pair $i,j\in [1,K]$ 대해서 아래와 같이 식을 쓸 수 있음.

$$\begin{array}{rl}\frac{\exp \left[({\mathbf{z}}_n^{(i)}-a_S)/b_S\right]}{\exp \left[({\mathbf{z}}_n^{(j)}-a_S)/b_S\right]}& =\frac{\exp \left[({\mathbf{v}}_n^{(i)}-a_T)/b_T\right]}{\exp \left[({\mathbf{v}}_n^{(j)}-a_T)/b_T\right]}\\ \to ({\mathbf{z}}_n^{(i)}-{\mathbf{z}}_n^{(j)})/b_S& =({\mathbf{v}}_n^{(i)}-{\mathbf{v}}_n^{(j)})/b_T\end{array}$$

• $j$에 대해서 average 하면, 즉, ${\bar{\mathbf{z}}}_n=1/K\sum _{m=1}^K{\mathbf{z}}_n^{(m)},{\bar{\mathbf{v}}}_n=1/K\sum _{m=1}^K{\mathbf{v}}_n^{(m)}$를 적용하면 아래와 같이 정리할 수 있음.

$$({\mathbf{z}}_n^{(i)}-{\bar{\mathbf{z}}}_n)/b_S=({\mathbf{v}}_n^{(i)}-{\bar{\mathbf{v}}}_n)/b_T$$

• 위의 식을 제곱하여 $i$에 대해서 average 하면, input logit vector에 대한 standard deviation $\sigma$로 표현되는 아래의 식으로 정리됨.

$$\frac{\sigma ({\mathbf{z}}_n{)}^2}{\sigma ({\mathbf{v}}_n{)}^2}=\frac{\frac{1}{K}\sum _{i=1}^K{({\mathbf{z}}_n^{(i)}-{\bar{\mathbf{z}}}_n)}^2}{\frac{1}{K}\sum _{i=1}^K{({\mathbf{v}}_n^{(i)}-{\bar{\mathbf{v}}}_n)}^2}=\frac{b_S^2}{b_T^2}$$

• 위의 식을 통해서, well-distilled student의 특성을 ① logit shift와 ② variance matching으로 나타낼 수 있음.

① Logit shift

$$({\mathbf{z}}_n^{(i)}-{\bar{\mathbf{z}}}_n)/b_S=({\mathbf{v}}_n^{(i)}-{\bar{\mathbf{v}}}_n)/b_T$$

$${\mathbf{z}}_n^{(i)}={\mathbf{v}}_n^{(i)}+{\mathrm{\Delta }}_n,\text{ where }{\mathrm{\Delta }}_n={\bar{\mathbf{z}}}_n-{\bar{\mathbf{v}}}_n$$

• 기존의 shared temperature를 적용 $(b_S=b_T)$하면 student와 teacher의 logit사이의 constant shift ${\mathrm{\Delta }}_n$가 존재함. 즉, traditional KD는 student가 teacher의 shifted logit를 모방하도록 함. 
• 하지만, 두 모델의 capacity 차이를 생각할 때, student는 teacher처럼 넓은 logit range를 얻을 수 없음. $($capacity가 logit range에 영향을 미침? → "Improving distillation for large teacher" 참고$)$
• 정확한 logit matching보다 logit rank만을 유지하면 되기 때문에, 기존 KD방법의 logit shift는 student에게 불필요한 어려움을 제공함.

② Variance match

$$\frac{\sigma ({\mathbf{z}}_n)}{\sigma ({\mathbf{v}}_n)}=\frac{b_S}{b_T}$$

• 위 식은 temperature ratio와 standard deviation ratio가 동일함을 의미함. 기존 shared temperature $b_S=b_T$는 $\sigma \left({\mathbf{z}}_n\right)=\sigma \left({\mathbf{v}}_n\right)$가 되도록 강제하기 때문에, student logit의 standard deviation을 제한함.

 

3) Logit Standardization

• 기존 shared temperature가 가지는 logit shift, variance match의 두 가지 단점을 극복하기 위해, $a_S,b_S,a_T,b_T$를 각 logit의 mean ${\bar{\mathbf{z}}}_n$과 weighted standard deviation $\sigma ({\mathbf{z}}_n)$으로 대체하여 Algo. 1과 같이 weighted $\mathcal{Z}$-score function을 구할 수 있음. 

$$q{({\mathbf{z}}_n;{\bar{\mathbf{z}}}_n,\sigma ({\mathbf{z}}_n))}^{(k)}=\frac{\exp (\mathcal{Z}({\mathbf{z}}_n;\tau {)}^{(k)})}{\sum _{m=1}^K\exp (\mathcal{Z}({\mathbf{z}}_n;\tau {)}^{(m)})}$$

$$q{({\mathbf{v}}_n;{\bar{\mathbf{v}}}_n,\sigma ({\mathbf{v}}_n))}^{(k)}=\frac{\exp (\mathcal{Z}({\mathbf{v}}_n;\tau {)}^{(k)})}{\sum _{m=1}^K\exp (\mathcal{Z}({\mathbf{v}}_n;\tau {)}^{(m)})}$$

• $\mathcal{Z}$-score standardization를 사용하면, ① zero mean, ② finite standard deviation, ③ monotonicity, ④ boundedness의 장점이 있음.

① Zero mean

• $\mathcal{Z}$-score function를 적용하면 standardized vector의 평균이 0이 됨.

② Finite standard deviation

• Weighted $\mathcal{Z}$-score output의 standard deviation은 $1/\tau$과 동일함.
• Standardized student와 teacher logit을 zero mean과 definite standard deviation을 가지는 Gaussian-like 분포로 표현가능함.
• Standardization의 mapping은 many-to-one이기 때문에 그 반대는 정의되지 않음. 즉, 기존 student logit vector의 variacne와 value range는 제한 없음.

③ Monotonicity

• $\mathcal{Z}$-score는 linear transformation function이기 때문에 monotonic function임. 즉, standardized student logit은 기존의 student logit과 같은 rank를 가짐.
• Teacher logit 내의 필수적인 고유 관계가 보존됨.

④ Boundedness

• Standardized logit은 $[-\sqrt{K-1}/\tau ,\sqrt{K-1}/\tau ]$으로 bounded 되며 이를 통해, 과도하게 큰 값을 피할 수 있음. logit range를 조절하기 위해 base temperature를 정의함.

Toy Case

• ${\mathcal{S}}_1$는 teacher prediction을 magnitude 측면에서 더욱 유사하게 예측했고, ${\mathcal{S}}_2$는 teacher의 rank를 그대로 유지했음. ${\mathcal{S}}_1$의 경우 ${\mathcal{S}}_2$보다 더 작은 KL divergence loss를 얻었지만, ${\mathcal{S}}_1$는 잘못된 예측을 했고, ${\mathcal{S}}_2$는 올바른 예측을 함. 이를 통해 loss 비교의 모순을 알 수 있음.
• $\mathcal{Z}$-score를 적용하면, 모든 logit이 re-scaled 되고 magnitude보다 relation이 강조됨. 정규화된 후, loss는 ${\mathcal{S}}_2$가 ${\mathcal{S}}_1$보다 낮아지는 것을 확인할 수 있음.

 

 

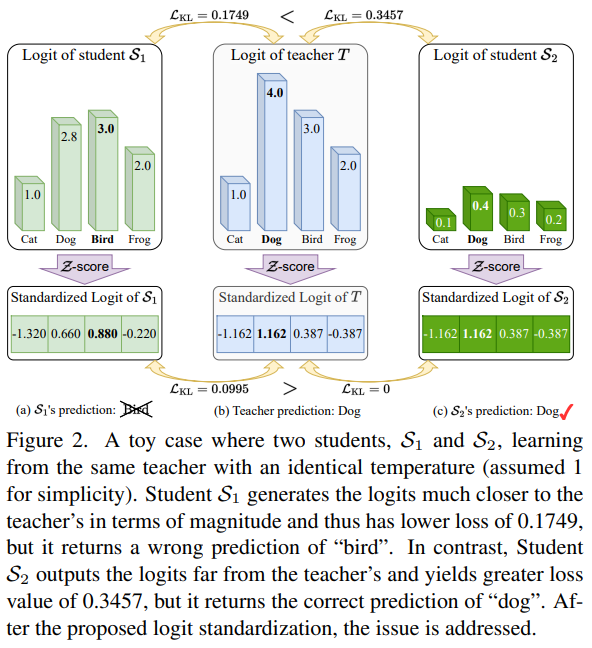
Experiments

Main Results

CIFAR-100

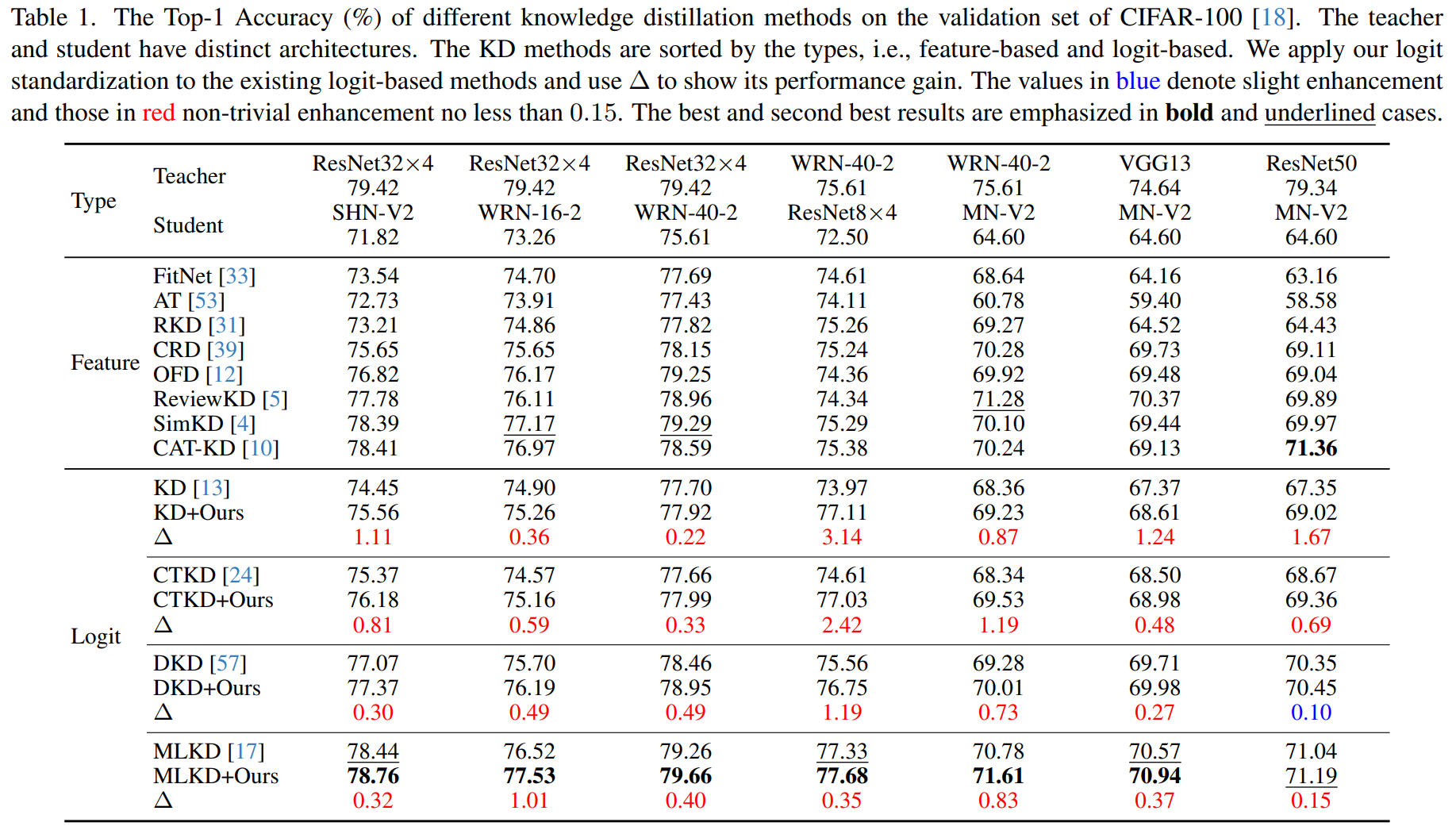
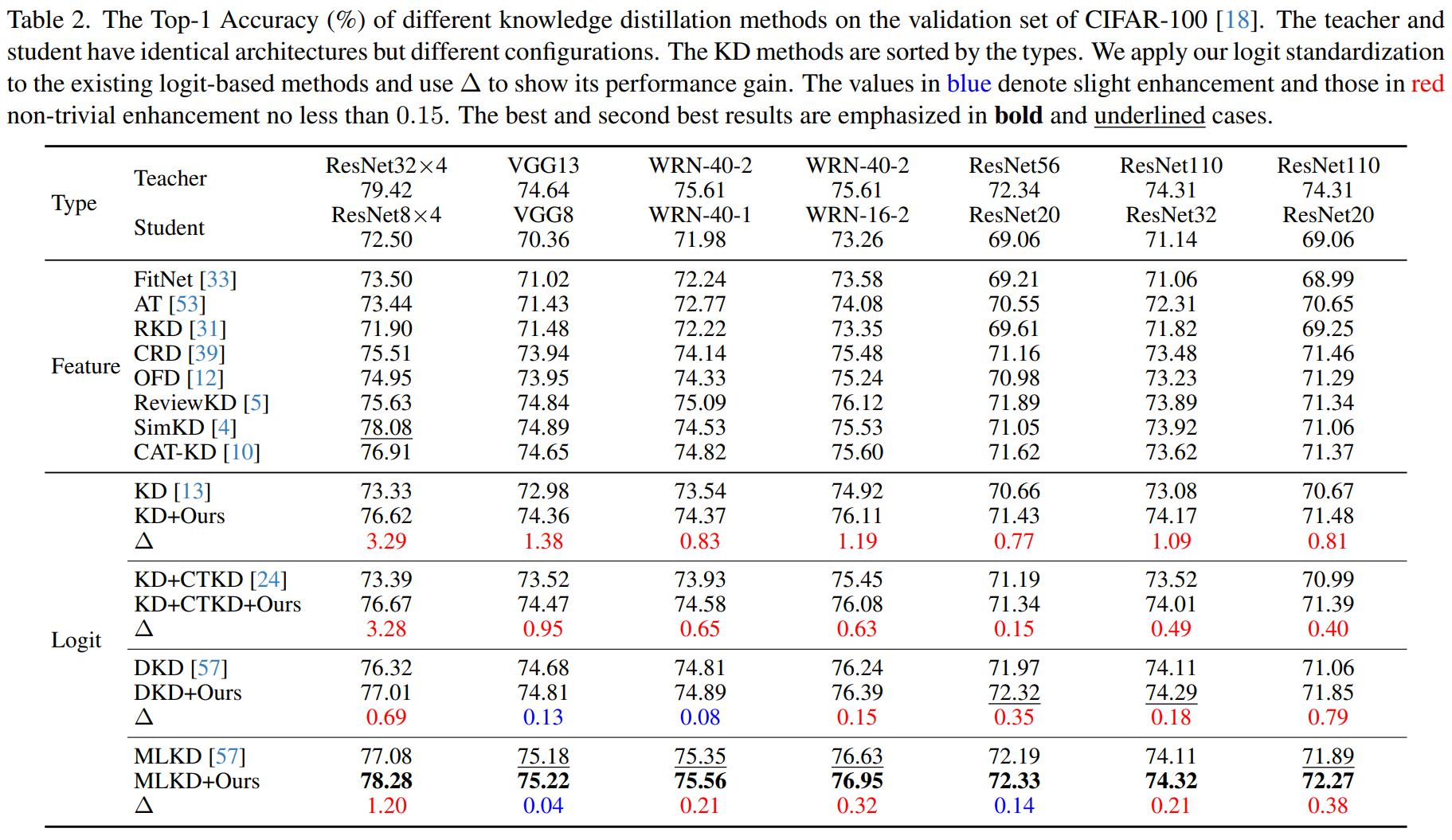
ImageNet

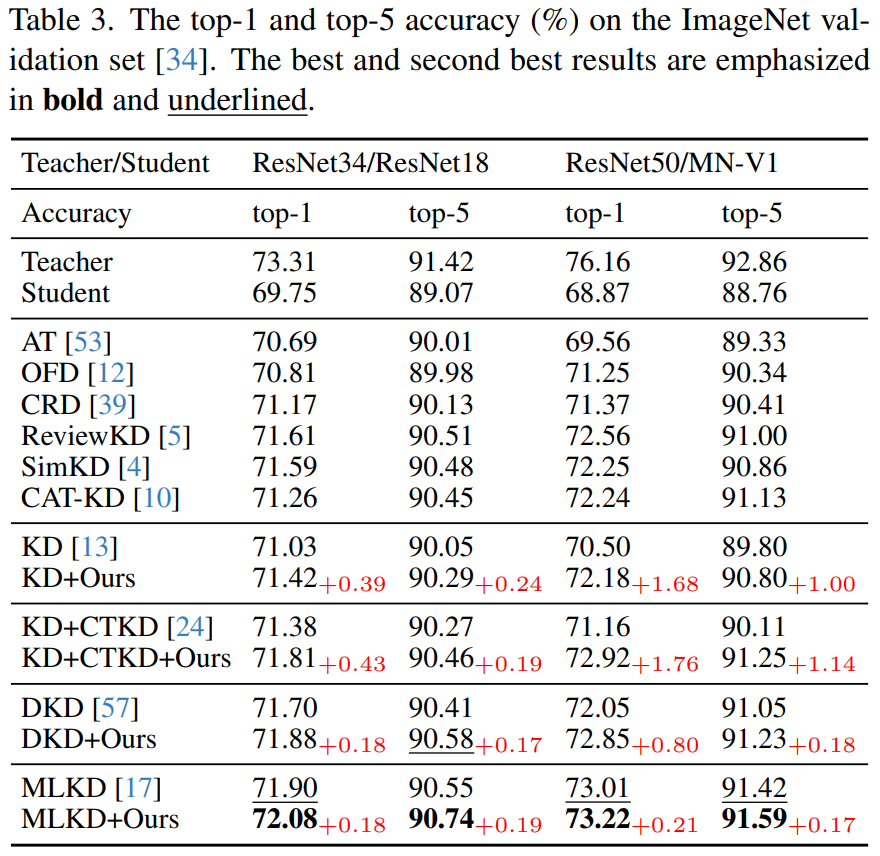
Ablation Study

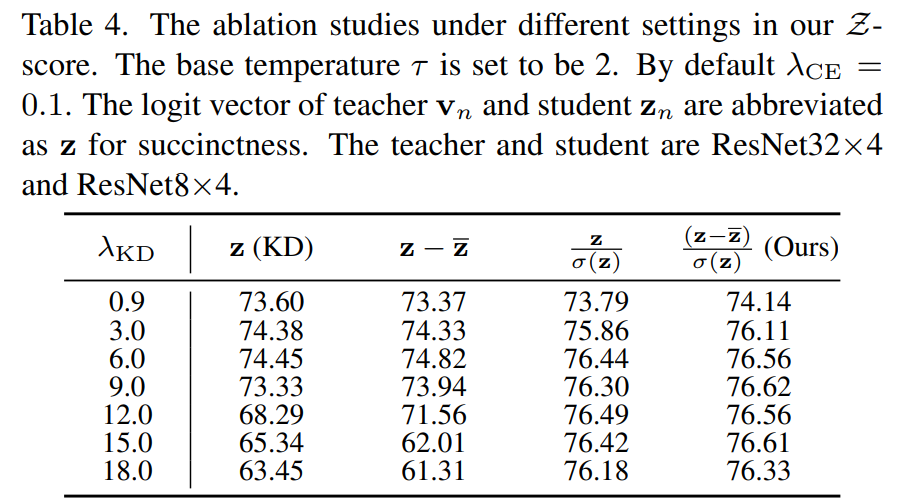
• KD loss의 weight가 증가할수록, vanilla KD의 성능은 급격히 하락하는 것에 반해, $\mathcal{Z}$-score pre-process는 향상된 성능을 얻을 수 있음.

 

Extensions

Logit range

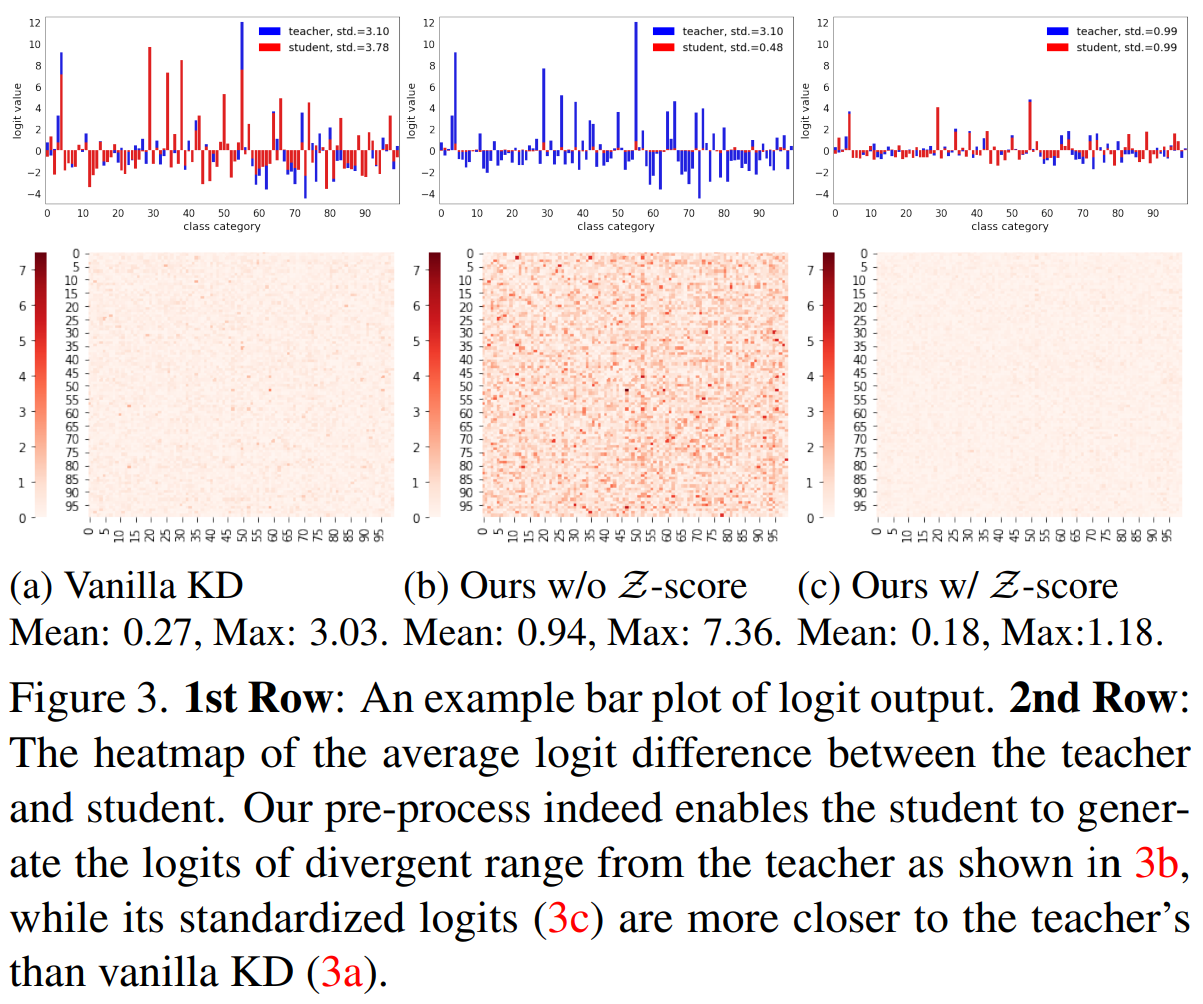
• 기존 KD를 적용하면, target index에 대해서 student가 teacher만큼의 large logit을 가질 수 없는 반면, 본 논문에서의 방법을 적용하면, 적절한 range의 logit을 만들어 teacher을 잘 모사하도록 함.

Logit variance

• 기존 KD는 student logit의 variance가 teacher의 variance로 접근하도록 하지만, 본 논문 방식은 student logit이 flexible logit variance를 가지도록 함. standardized logit은 teacher와 동일한 variance를 가짐.

Feature visualizations

Improving distillation for large teacher

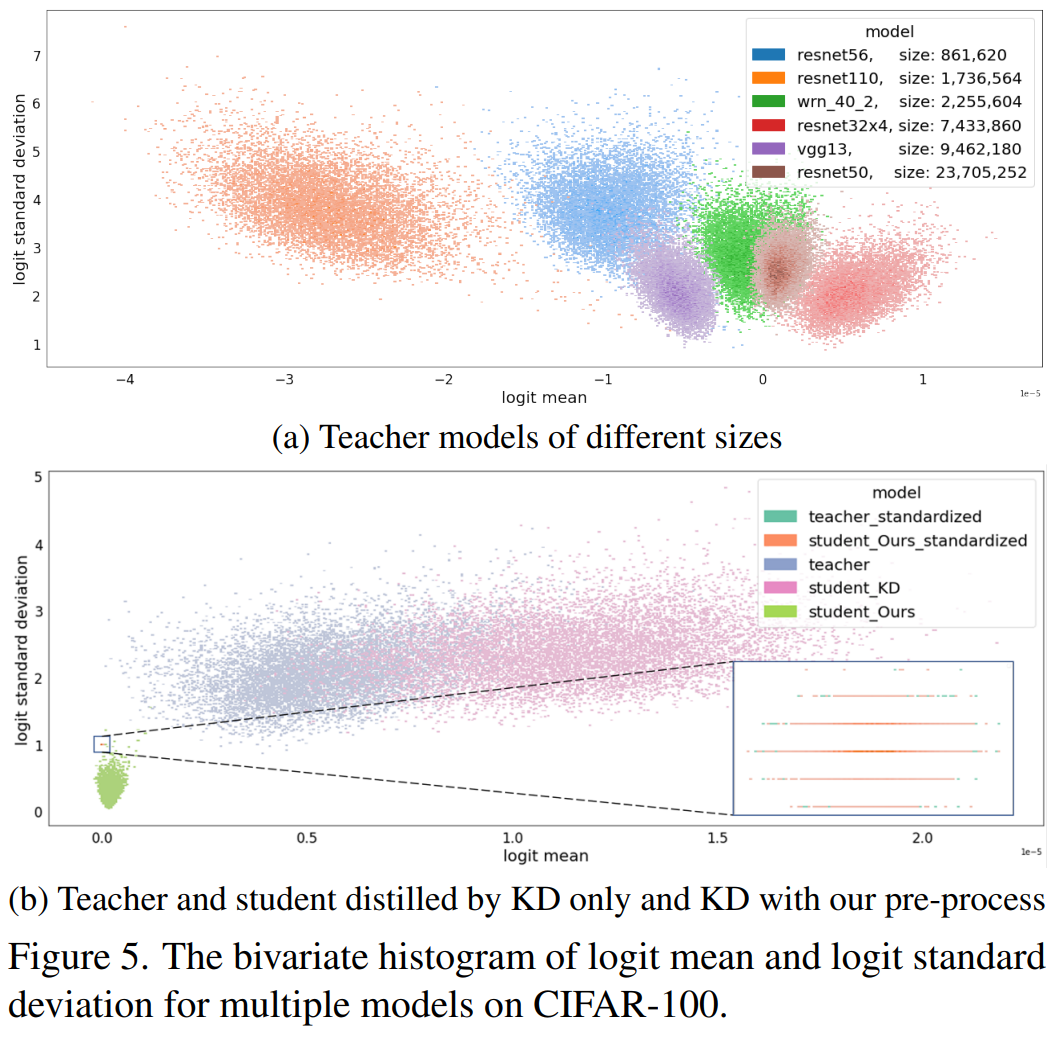
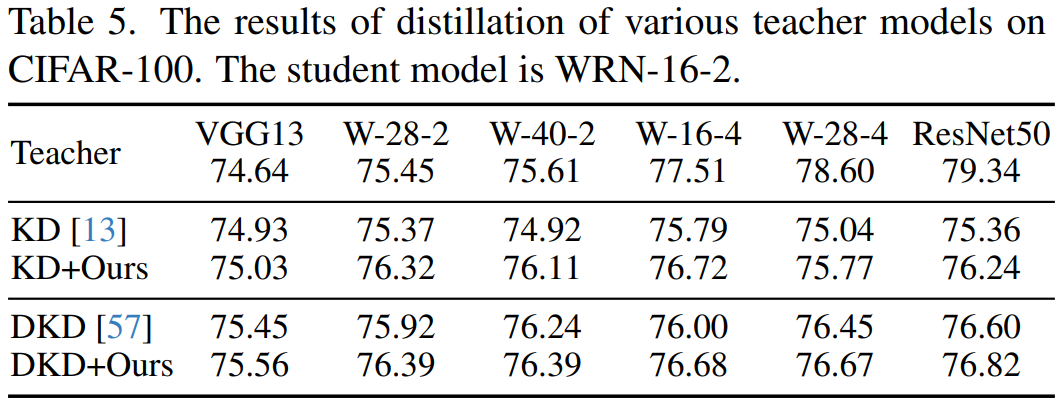
• 큰 teacher가 언제나 좋은 teacher를 의미하는 것이 아니며, 이는 teacher와 student 간의 capacity gap으로부터 기인한다고 설명되어 옴.
• 본 논문에서는 이를 student가 teacher와 동일한 logit range와 variance를 모사하기 어렵기 때문이라고 해석하고 이를 시각적으로 확인하고자 그림 5를 얻음.
• 그림 5를 보면, 큰 model$($e.g., ResNet50, VGG13$)$ 일수록 logit이 zero mean에 가깝고 작은 standard deviation를 가짐. 반대로, 작은 model의 경우, zero mean에서 많이 떨어져 있고, 큰 variacne를 가짐.  $($resnet56와 resnet110의 경우에는 반대 결과처럼 보이는 데, 왜 그러지?$)$
• 따라서, 작은 model인 student가 큰 model인 teacher 만큼 compact logit을 얻는 것은 어려움.
• 그림 5 b를 통해서, student의 모방 능력을 비교할 수 있음. logit mean과 standard deviation에 대해서 vanilla KD는 teacher와 상당 부분 떨어진 logit을 만들어내는 반면, standardized logit mean과 standard deviation에 대해, 제안 방법은 완전한 일치를 보여줌.

 

 

Conclusions

• Conventional KD에서 global 하고 shared temperature를 사용하는 이론적 근거가 없었기 때문에, entropy maximization을 사용하여, temperature가 Lagrangian multiplier으로부터 유도됨을 보였고, 이를 통해 constant temperature대신 flexible value를 할당할 수 있음을 증명함. 이를 기반으로 $\mathcal{Z}$-score standardization을 pre-process로 제안하여, teacher가 가지는 본질적인 relation을 집중적으로 학습하게 만들었음.